【题目】等边△ABC中，点H在边BC上，点K在边AC上，且满足AK=HC，连接AH、BK交于点F,

(1)如图1，求∠AFB的度数；

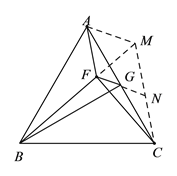
(2)如图2，连接FC，若∠BFC=90°，点G为边 AC上一点，且满足∠GFC=30°，求证：AG⊥BG;

参考答案：

【答案】(1) ;(2)证明见解析

【解析】

（1）易得：≌ 即可求出的度数.

（2）)在BF上取M使AF=FM，连MC延长FG交MC于N,可得△AFM是等边三角形，可证△AFB≌△AMC，再证△AGF≌△CGN，可得是的中点，可以根据等腰三角形三线合一的性质解答即可.

解：（1)在等边△ABC中：AB=AC,∠BAK=∠C=60°

在△ABK和△CAH中，

∴≌

(2)在BF上取M使AF=FM，连MC延长FG交MC于N,

∵

∴

∴△AFM是等边三角形

∴AF=AM, ∠FAM=60°

又∵∠BAC=60°

∴∠BAF=∠CAM

又∵AB=AC

∴△AFB≌△AMC，

∴∠AMC=∠AFC= 120°,

又△AFM为等边三角形，

∴∠AMB=∠BMC=60°,

∵∠BFC=90°，

∴∠MFC=90°，∠NFC=30°,

∴△FMN为等边三角形，且FN=NC,

∴NC=FN=FM=AF，

∴△AGF≌△CGN,

∴AG=GC，

又∵AB=BC

∴BG⊥AC,

关闭