[题目]在平面直角坐标系中.点P(m.n)在第一象限.且在直线y=-x+6上.点A的坐标为(5,0).O是坐标原点.△PAO的面积是S.(1)求S与m的函数关系式.并画出函数S的图象,(2)小杰认为△PAO的面积可以为15.你认为呢? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】在平面直角坐标系中，点P（m，n）在第一象限，且在直线y=-x+6上，点A的坐标为（5,0），O是坐标原点，△PAO的面积是S.

（1）求S与m的函数关系式，并画出函数S的图象；

（2）小杰认为△PAO的面积可以为15，你认为呢？

【答案】（1）S，图象见解析；（2）（0,6）.

【解析】试题分析：（1）根据P点的坐标，可得到点P到x轴的距离，然后根据三角形的面积公式可得到函数的解析式；

（2）把面积的值代入函数的解析式，求出P点的坐标，进而可判断.

试题解析：（1）∵P(m,n)在直线y=-x+6上，且在第一象限，

∴n=-m+6，即：点P到x轴距离为-m+6，

∵点A坐标为（5,0），

∴

图象如下：

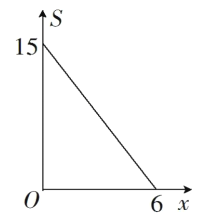
（2）若S=15，即，

解得m=0 ，

此时点P的坐标为（0,6）.

所以这时的三角形不存在，因此△PAO的面积不可以为15.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】在△ABC中，AB=AC，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．

（1）如图1，当点D在线段CB上，且∠BAC=90°时，那么∠DCE= 度；

（2）设∠BAC= ，∠DCE= ．

① 如图2，当点D在线段CB上，∠BAC≠90°时，请你探究与之间的数量关系，并证明你的结论；

② 如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整，并直接写出此时与之间的数量关系（不需证明）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，△ABO中，AB⊥OB，OB= ，AB=1，把△ABO绕点O旋转150°后得到△A1B1O，则点A1的坐标为（）

A.（﹣1，）
B.（﹣1，）或（﹣2，0）
C.（，﹣1）或（0，﹣2）
D.（，﹣1）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】体育课上，体育老师对七年级一个班的学生进行了立定跳远项目的测试，得到一组测试分数的数据，并将测试所得分数绘制如图所示的统计图，图中从左到右的学生数人数之比为2 : 3 : 4 : 1，且成绩为8分的学生有12人，根据以上信息解答下列问题：

(1) 这个班级有多少名学生？

（2）这组数据的众数是分，中位数是分.

（3）这个班级学生立定跳远项目测试的平均成绩是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】计算：

（1）45+（﹣20）；

（2）（﹣8）﹣（﹣1）；

（3）|﹣10|+|+8|；

（4）（﹣12）﹣5+（﹣14）﹣（﹣39）；

（5）0.47﹣4﹣（﹣1.53）﹣1；

（6）36﹣76+（﹣23）﹣105；

（7）﹣20+|﹣14|﹣（﹣18）﹣13；

（8）（+1.75）+（﹣）+（+）+（+1.05）+（﹣）+（+2.2）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，经过点A（0，﹣4）的抛物线y= x2+bx+c与x轴相交于点B（﹣1，0）和C，O为坐标原点．

（1）求抛物线的解析式；
（2）将抛物线y= x2+bx+c向上平移个单位长度，再向左平移m（m＞0）个单位长度，得到新抛物线，若新抛物线的顶点P在△ABC内，求m的取值范围；
（3）将x轴下方的抛物线图象关于x轴对称，得到新的函数图象C，若直线y=x+k与图象C始终有3个交点，求满足条件的k的取值范围．