【题目】在平面直角坐标系中,直线y=x-1经过( )
A. 第一、二、三象限 B. 第一、二、四象限
C. 第一、三、四象限 D. 第二、三、四象限
参考答案:
【答案】C
【解析】根据一次函数y=kx+b图象的性质判断即可.即:k>0,经过第一、三象限;k<0,经过第二、四象限;b>0,交y轴正半轴;b<0,交y轴负半轴;
因为直线y=x-1中,x的系数1>0,
所以,直线经过第一、三象限,
因为-1<0,所以,直线与y轴负半轴相交,
所以,直线y=x-1经过第一、三、四象限.
故选:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A1(1,2),A2(2,5),A3(3,10),A4(4,17),…,用你发现的规律确定点An的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:三角形三条内角平分线的交点叫做三角形的内心;
性质:内心到三角形三边的距离相等.
如图1,点 为
为  的内心,
的内心,  于
于 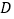 ,
,  于E,
于E,  于
于 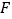 ,则有
,则有  .
.
问题:如何求 的值呢?
的值呢?
探究:
(1)小明思路:设△ABC的面积为 ,
,  的面积为
的面积为 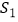 ,
,  的面积为
的面积为  ,
,  的面积为
的面积为  ,利用
,利用  可求
可求  .
.
①图1中, ,
, 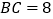 ,
,  ,
,  ,请你根据小明的思路求出
,请你根据小明的思路求出  的值;
的值;
②如图2,△ABC中,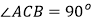 ,设
,设  ,
,  ,
,  ,
,  为 △ABC的内心,
为 △ABC的内心,  于
于 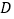 ,
,  于E,
于E,  于
于 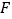 .若设
.若设  ,请用含
,请用含  ,
,  ,
, 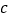 的式子表示
的式子表示 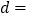 ;
;
(2)小亮思路:“凡角平分处,必有轴对称”. 如图2,易得: ,
,  ,
,  . 请你根据小亮的思路,用含
. 请你根据小亮的思路,用含  ,
,  ,
, 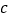 的式子表示
的式子表示 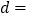 ;
;
(3)①根据上述所列两式,求证: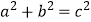 ;
;
②应用:已知一个直角三角形的两直角边长分别为 和
和  ,求该三角形的内心到任意一边的距离
,求该三角形的内心到任意一边的距离  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的周长为20cm,底边长为ycm,腰长为xcm,y与x之间的函数表达式为y=20-2x,则自变量x的取值范围是__________.
-
科目: 来源: 题型:
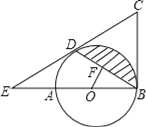
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需________根火柴( )

A. 156 B. 157 C. 158 D. 159
相关试题

