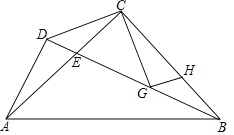
【题目】如图△ABC中,CA=CB,∠ACB=90°,D为△ABC外一点,且AD⊥BD,BD交AC于E,G为BC上一点,且∠BCG=∠DCA,过G点作GH⊥CG交CB于H.
(1)求证:CD=CG;
(2)若AD=CG,求证:AB=AC+BH.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据等腰直角三角形的性质可得∠BAC=∠ABC=45°,然后求出∠DAC=∠GBC,再利用“角边角”证明△ACD和△BCG全等,根据全等三角形对应边相等证明即可;
(2)延长CG交AB于F,求出△CDG是等腰直角三角形,根据等腰直角三角形的性质可得∠CGD=45°,然后求出∠BGH=∠BGF,再求出BG=CG,根据等边对等角可得∠BCG=∠CBG,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CBG=22.5°,再求出∠GBF=22.5°,从而得到∠CBG=∠GBF,利用“角边角”证明△BGF和△BGH全等,根据全等三角形对应边相等可得BH=BF,再求出∠ACF=∠AFC=67.5°,根据等角对等边可得AC=AF,然后根据AB=AF+BF等量代换即可得证.
证明:(1)∵CA=CB,∠ACB=90°,
∴∠BAC=∠ABC=45°,
∵AD⊥BD,
∴∠DAC+45°+∠ABD=90°,
∴∠DAC+∠ABD=45°,
∵∠GBC+∠ABD=∠ABC=45°,
∴∠DAC=∠GBC,
在△ACD和△BCG中,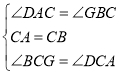 ,
,
∴△ACD≌△BCG(ASA),
∴CD=CG;
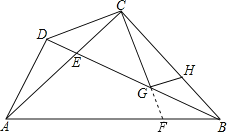
(2)如图,延长CG交AB于F,
∵∠BCG=∠DCA,
∴∠DCG=∠DCA+∠ACG=∠BCG+∠ACG=∠ACB=90°,
又∵CD=CG,
∴△CDG是等腰直角三角形,
∴∠CGD=45°,
∵GH⊥CG,∠BGF=∠CGD(对顶角相等),
∴∠BGH=∠BGF,
∵△ACD≌△BCG,
∴AD=BG,
∵AD=CG,
∴BG=CG,
∴∠BCG=∠CBG,
由三角形的外角性质,∠BGF=∠BCG+∠CBG=45°,
∴∠CBG=22.5°,
∴∠GBF=∠ABC﹣∠CBG=45°﹣22.5°=22.5°,
∴∠CBG=∠GBF,
在△BGF和△BGH中,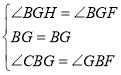 ,
,
∴△BGF≌△BGH(ASA),
∴BH=BF,
又∵∠AFC=∠ABD+∠BGF=22.5°+45°=67.5°,
∴∠ACF=180°﹣∠BAC﹣∠AFC=180°﹣45°﹣67.5°=67.5°,
∴∠ACF=∠AFC=67.5°,
∴AC=AF,
∵AB=AF+BF,
∴AB=AC+BH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2
 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD内接于圆O,∠BAD=60°,AC为圆O的直径.AC交BD于P点且PB=2,PD=4,则AD的长为( )

A. 2
 B. 2
B. 2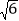 C. 2
C. 2 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形的边AD,点D落在BC边的点F处,AB=8cm,BC=10cm,求△ECF的周长.
-
科目: 来源: 题型:
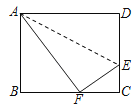
查看答案和解析>>【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了,有一种用“因式分解”法产生的密码、方便记忆,其原理是:将一个多项式分解因式,如多项式:
 因式分解的结果为
因式分解的结果为 ,当
,当 时,
时, 此时可以得到数字密码171920.
此时可以得到数字密码171920.(1)根据上述方法,当
 时,对于多项式
时,对于多项式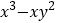 分解因式后可以形成哪些数字密码?(写出三个)
分解因式后可以形成哪些数字密码?(写出三个)(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为x、y,求出一个由多项式
 分解因式后得到的密码(只需一个即可);
分解因式后得到的密码(只需一个即可);(3)若多项式
 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当 时可以得到其中一个密码为242834,求m、n的值.
时可以得到其中一个密码为242834,求m、n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90 ,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
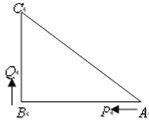
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD、CM分别是斜边上的高和中线,那么下列结论中错误的是( )
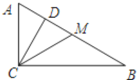
A.CM=ACB.∠ACM=∠DCBC.AD=DMD.DB=4AD
相关试题

