【题目】有一张等腰三角形纸片,AB=AC=5,BC=3,小明将它沿虚线PQ剪开,得到△AQP和四边形BCPQ两张纸片(如图所示),且满足∠BQP=∠B,则下列五个数据![]() ,3,
,3,![]() ,2,
,2,![]() 中可以作为线段AQ长的有 个.
中可以作为线段AQ长的有 个.

参考答案:
【答案】3.
【解析】
试题分析:作CD∥PQ,交AB于D,如图所示:
则∠CDB=∠BQP,∵AB=AC=5,∴∠B=∠ACB,∵∠BQP=∠B,∴∠B=∠ACB=∠CDB,∴CD=BC=3,△BCD∽△BAC,∴![]() ,即
,即![]() ,解得:BD=
,解得:BD=![]() ,∴AD=AB﹣BD=
,∴AD=AB﹣BD=![]() ,∵CD∥PQ,∴△APQ∽△ACD,∴
,∵CD∥PQ,∴△APQ∽△ACD,∴![]() ,即
,即 ,解得:AP=
,解得:AP=![]() AQ,当AQ=
AQ,当AQ=![]() 时,AP=
时,AP=![]() ×
×![]() =
=![]() >5,不合题意,舍去;
>5,不合题意,舍去;
当AQ=3时,AP=![]() ×3=
×3=![]() <5,符合题意;
<5,符合题意;
当AQ=![]() 时,点P与C重合,不合题意,舍去;
时,点P与C重合,不合题意,舍去;
当AQ=2时,AP=![]() ×2=
×2=![]() <5,符合题意;
<5,符合题意;
当AQ=![]() 时,AP=
时,AP=![]() ×
×![]() =
=![]() <5,符合题意;
<5,符合题意;
综上所述:可以作为线段AQ长的有3个;
故答案为:3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度,随机抽取了部分学生进行调查(每人限选1项),现将调查结果绘制成如下两幅不完整的统计图,根据图中所给的信息解答下列问题.
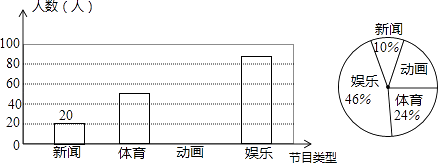
(1)喜爱动画的学生人数和所占比例分别是多少?
(2)请将条形统计图补充完整;
(3)若该校共有学生1000人,依据以上图表估计该校喜欢体育的人数约为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】“翻开八年级数学课本,恰好翻到第28页”,这个事件是( )
A. 必然事件 B. 随机事件 C. 不可能事件 D. 确定事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O.

(1)求证:OB=OC.
(2)若∠ABC=65°,求∠COD的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2+x﹣2与y轴交点的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数的图象经过点(0,3),顶点坐标为(1,4).
(1)求这个二次函数的解析式;
(2)若将该抛物线绕原点旋转180°,请直接写出旋转后的抛物线函数表达式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD于H,点O是AB中点,连接OH,则OH= .

相关试题

