【题目】第三届世界互联网大会(3rd World Internet Conference),是由中华人民共和国倡导并举办的互联网盛会,于2016年11月16日至18日在浙江乌镇举办.某初中学校为了了解本校学生对本次互联网大会的关注程度(关注程度分为:A.特别关注;B.一般关注;C.偶尔关注;D.不关注),随机抽取了部分学生进行调查,并将结果绘制成频数折线统计图1和扇形统计图2(不完整)请根据图中信息回答问题.
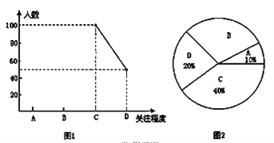
(1)此次抽样调查中,共调查了多少名学生?
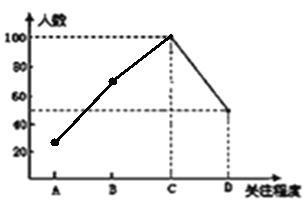
(2)求出图2中扇形B所对的圆心角度数,并将图1补充完整.
(3)在这次调查中,九(1)班共有甲、乙、丙、丁四人“特别关注”本届互联网大会,现准备从四人中随机抽取两人进行交流,请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率.
参考答案:
【答案】(1)250; (2)108 图1补充见解析;(3)列表或树状图见解析,P(抽取甲乙)=![]() .
.
【解析】试题分析:(1)根据题意,用偶尔关注的人数除以偶尔关注的比例即可求解;
(2)由扇形统计图即可求出扇形B所对的圆心角度数,然后再计算A、B的人数,补全图形即可;
(3)列表或画树状图得出所有等可能的情况数,找出恰好是甲与乙的情况,即可确定出所求概率.
试题解析:(1)100÷40%=250
∴共调查了250名学生.
(2)1-20%-10%-40%=30%
360°×30%=108°
∴扇形B所对的圆心角度数是108
250×10%=25;
250×30%=75
补图如下:
(3)列表如下(或树状图):
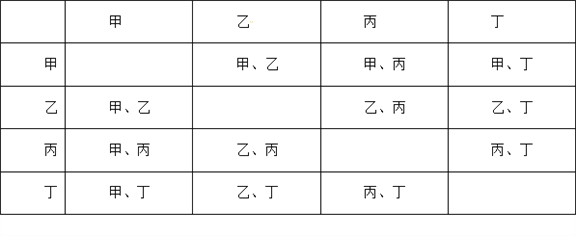
共有12种等可能的结果数,其中含甲和乙的结果数为2,
所以九(1)班抽取的两人恰好是甲和乙的概率.
P(抽取甲乙)=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,且c为有理数,则( )
A. ac>bc B. ac<bc C. ac2>bc2 D. ac2≥bc2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
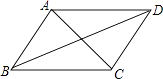
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】采摘茶叶是茶农一项很繁重的劳动,利用单人便携式采茶机能大大提高生产效率.实践证明,一台采茶机每天可采茶60公斤,是人手工采摘的5倍,购买一台采茶机需2400元.茶园雇人采摘茶叶,按每采摘1公斤茶叶m元的标准支付雇工工资,一个雇工手工采摘茶叶20天获得的全部工钱正好购买一台采茶机.
(1)求m的值;
(2)有两家茶叶种植户王家和顾家均雇人采摘茶叶,王家雇用的人数是顾家的2倍.王家所雇的人中有
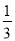 的人自带采茶机采摘,
的人自带采茶机采摘, 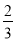 的人手工采摘,顾家所雇的人全部自带采茶机采摘.某一天,王家付给雇工的工资总额比顾家付给雇工的工资总额少600元.问顾家当天采摘了多少公斤茶叶?
的人手工采摘,顾家所雇的人全部自带采茶机采摘.某一天,王家付给雇工的工资总额比顾家付给雇工的工资总额少600元.问顾家当天采摘了多少公斤茶叶? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A与点B关于x轴对称,若点A的坐标为(2,3),则点B所在的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
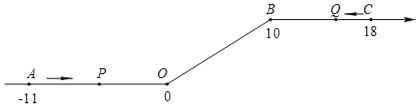
问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+mx+5=0的一个解是x=1,则m=_____.
相关试题

