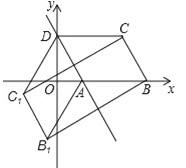
【题目】如图,已知ABCD的三个顶点A(n,0)、B(m,0)、D(0,2n)(m>n>0),作ABCD关于直线AD的对称图形AB1C1D.
(1)若m=3,试求四边形CC1B1B面积S的最大值;
(2)若点B1恰好落在y轴上,试求![]() 的值.
的值.
参考答案:
【答案】(1)9;(2)![]() .
.
【解析】
试题分析:(1)如图1,易证SBCEF=SBCDA=SB1C1DA=SB1C1EF,从而可得SBCC1B1=2SBCDA=![]() ,根据二次函数的最值性就可解决问题;
,根据二次函数的最值性就可解决问题;
(2)如图2,易证△AOD∽△B1OB,根据相似三角形的性质可得OB1=![]() ,然后在Rt△AOB1中运用勾股定理就可解决问题.
,然后在Rt△AOB1中运用勾股定理就可解决问题.
试题解析:(1)如图1,∵ABCD与四边形AB1C1D关于直线AD对称,∴四边形AB1C1D是平行四边形,CC1⊥EF,BB1⊥EF,∴BC∥AD∥B1C1,CC1∥BB1,∴四边形BCEF、B1C1EF是平行四边形,∴SBCEF=SBCDA=SB1C1DA=SB1C1EF,∴SBCC1B1=2SBCDA.
∵A(n,0)、B(m,0)、D(0,2n)、m=3,∴AB=m﹣n=3﹣n,OD=2n,∴SBCDA=ABOD=(3﹣n)2n=![]() =
=![]() ,∴SBCC1B1=2SBCDA=
,∴SBCC1B1=2SBCDA=![]() .
.
∵﹣4<0,∴当n=![]() 时,SBCC1B1最大值为9;
时,SBCC1B1最大值为9;
(2)当点B1恰好落在y轴上,如图2,∵DF⊥BB1,DB1⊥OB,∴∠B1DF+∠DB1F=90°,∠B1BO+∠OB1B=90°,∴∠B1DF=∠OBB1.
∵∠DOA=∠BOB1=90°,∴△AOD∽△B1OB,∴![]() ,∴
,∴![]() ,∴OB1=
,∴OB1=![]() .
.
由轴对称的性质可得AB1=AB=m﹣n.在Rt△AOB1中,![]() ,整理得
,整理得![]() .
.
∵m>0,∴3m﹣8n=0,∴![]() =
=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(2x+3)(x﹣4)﹣x(x+2)﹣5,其中x=﹣2.
-
科目: 来源: 题型:
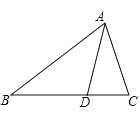
查看答案和解析>>【题目】如图,D是△ABC的BC边上的一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知9y2+my+1是完全平方式,则常数m的值是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学进行数字猜谜游戏:甲说一个数a的相反数就是它本身,乙说一个数b的倒数也等于本身,请你猜一猜|a﹣b|=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x-9)(2x-n)=2x2+mx-18,则m、n的值分别是( )
A. m=-16,n=-2B. m=16,n=-2C. m=-16,n=2D. m=16,n=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线
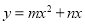 相交于A(1,
相交于A(1,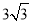 ),B(4,0)两点.
),B(4,0)两点.(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN,求出
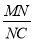 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.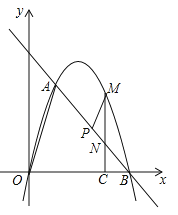
相关试题

