[题目]如图.在平面直角坐标系中.直线与反比例函数在第二象限内的图象相交于点．(1)求反比例函数的解析式,(2)将直线向上平移后与反比例函数图象在第二象限内交于点.与轴交于点.且的面积为.求直线的解析式．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在平面直角坐标系中，直线与反比例函数在第二象限内的图象相交于点．

(1)求反比例函数的解析式；

(2)将直线向上平移后与反比例函数图象在第二象限内交于点，与轴交于点，且的面积为，求直线的解析式．

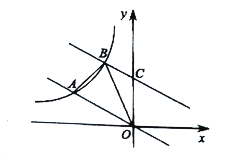
【答案】（1）；（2）

【解析】

（1）将A点坐标代入直线中求出m的值，确定出A的坐标，将A的坐标代入反比例解析式中求出k的值，即可确定出反比例函数的解析式；

（2）根据直线的平移规律设直线BC的解析式为，由同底等高的两三角形面积相等可得△ACO与△ABO面积相等，根据△ABO的面积为列出方程OC2=，解方程求出OC=，即b=，进而得出直线BC的解析式．

解：(1)：直线过点，

，解得．

．

∵反比例函数的图象过点，

．

∴反比例函数的解析式为

(2)设直线BC的解析式为，

与面积相等，且的面积为

的面积

∴直线的解析式为

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，已知∠MON及其边上一点A，以点A为圆心，AO长为半径画弧，分别交OM，ON于点B和C，再以点C为圆心，AC长为半径画弧，恰好经过点B，错误的结论是（）.

A.B.∠OCB＝90°C.∠MON＝30°D.OC＝2BC

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某体育看台侧面的示意图如图所示，观众区AC的坡度i为1：2，顶端C离水平地面AB的高度为10m，从顶棚的D处看E处的仰角α＝18°30′，竖直的立杆上C、D两点间的距离为4m，E处到观众区底端A处的水平距离AF为3m．

求：（1）观众区的水平宽度AB；

（2）顶棚的E处离地面的高度EF．（sin18°30′≈0.32，tanl8°30′≈0.33，结果精确到0.1m）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】甲、乙两人进行射击比赛，两人4次射击的成绩（单位：环）如下：

甲：8，6，9，9；

乙：7，8，9，8．

（1）请将下表补充完整：

	平均数	众数	中位数	方差
甲	8			1.5
乙		8	8

（2）谁的成绩较稳定？为什么？

（3）分别从甲、乙两人的成绩中随机各选取一次，则选取的两个成绩之和为16环的概率是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，二次函数y=ax2+bx+c的图象经过点A（﹣1，0）、点B（3，0）、点C（4，y1），若点D（x2，y2）是抛物线上任意一点，有下列结论：

①二次函数y=ax2+bx+c的最小值为﹣4a；

②若﹣1≤x2≤4，则0≤y2≤5a；

③若y2＞y1，则x2＞4；

④一元二次方程cx2+bx+a=0的两个根为﹣1和

其中正确结论的个数是（　　）

A. 1 B. 2 C. 3 D. 4

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，AB=AC，以AB为直径作半圆O，交BC于点D，连接AD，过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．

（1）求证：EF是⊙O的切线．

（2）如果⊙O的半径为5，sin∠ADE=，求BF的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】“勤劳”是中华民族的传统美德，学校要求同学们在家里帮助父母做一些力所能及的家务．在本学期开学初，小颖同学随机调查了部分同学寒假在家做家务的总时间，设被调查的每位同学寒假在家做家务的总时间为x小时，将做家务的总时间分为五个类别：A（0≤x＜10），B（10≤x＜20），C（20≤x＜30），D（30≤x＜40），E（x≥40）．并将调查结果制成如下两幅不完整的统计图：