【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. 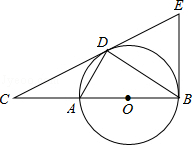
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.
参考答案:
【答案】
(1)证明:连结OD,
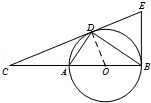
∵OB=OD,
∴∠OBD=∠BDO,
∵∠CDA=∠CBD,
∴∠CDA=∠ODB,
又∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,
即∠CDO=90°,
∴OD⊥CD,
∵OD是⊙O半径,
∴CD是⊙O的切线
(2)解:∵∠C=∠C,∠CDA=∠CBD
∴△CDA∽△CBD
∴ ![]()
∵ ![]() ,BC=6,
,BC=6,
∴CD=4,
∵CE,BE是⊙O的切线
∴BE=DE,BE⊥BC
∴BE2+BC2=EC2,即BE2+62=(4+BE)2
解得:BE= ![]()
【解析】(1)连OD,OE,根据圆周角定理得到∠ADO+∠ODB=90°,而∠CDA=∠CBD,∠CBD=∠ODB,于是∠CDA+∠ADO=90°;(2)根据已知条件得到△CDA∽△CBD由相似三角形的性质得到 ![]() ,求得CD=4,由切线的性质得到BE=DE,BE⊥BC根据勾股定理列方程即可得到结论.
,求得CD=4,由切线的性质得到BE=DE,BE⊥BC根据勾股定理列方程即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+
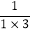 )(1+
)(1+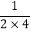 )(1+
)(1+ )(1+
)(1+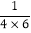 )…(1+
)…(1+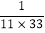 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料并解决有关问题:
我们知道:|x|=
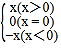 .现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
.现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:①x<﹣1;②﹣1≤x<2;③x≥2.
从而化简代数式|x+1|+|x﹣2|可分以下3种情况:
①当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②当﹣1≤x<2时,原式=x+1﹣(x﹣2)=3;
③当x≥2时,原式=x+1+x﹣2=2x﹣1.综上讨论,原式=
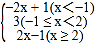 .
.通过以上阅读,请你解决以下问题:
(1)化简代数式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:
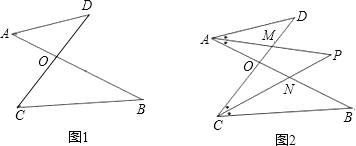
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数: 个;
(3)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.利用(1)的结论,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1(注:与图2完全相同),二次函数y=
 x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.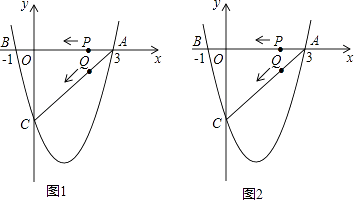
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折线ABCDE描述了一辆汽车在某一直线上行驶过程中,汽车离出发地的距离y(km)和行驶时间x(h)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120km;②汽车在行驶途中停留了0.5h;③汽车在整个行驶过程中的平均速度为
 km/h;④汽车自出发后3h~4.5h之间行驶的速度在逐渐减小.其中正确的说法是 .(填上所有正确的序号)
km/h;④汽车自出发后3h~4.5h之间行驶的速度在逐渐减小.其中正确的说法是 .(填上所有正确的序号) 
相关试题

