Question

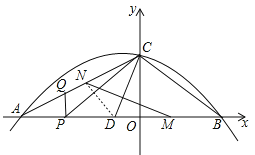
【题目】如图，抛物线y=ax2+bx+c为x轴的一交点为A（﹣6，0），与y轴的交点为C（0，3），且经过点G（﹣2，3）．

(1)求抛物线的表达式.

(2)点P是线段OA上一动点，过P作平行于y轴的直线与AC交于点Q，设△CPQ的面积为S，求S的最大值.

(3)若点B是抛物线与x轴的另一定点，点D、M在线段AB上，点N在线段AC上，∠DCB=∠CDB，CD是MN的垂直平分线，求点M的坐标．

Answer 1

【答案】（1）；（2）；（3）M（，0）．

【解析】试题分析：（1）把A、C、G三点坐标代入可求得抛物线解析式；

（2）先求直线AC的解析式，设P（x，0），可表示出OP、PQ，则可表示出S，再由二次函数的性质可求得S的最大值；

（3）由已知求得BD=BC=5，从而得到D点坐标，连接DN，可得出DN∥BC，从而DN为△ABC的中位线，得到DM的长，从而得到OM的长，进一步求得M点的坐标．

试题解析：（1）把A、C、G三点坐标代入抛物线解析式可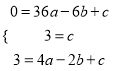得： ，解得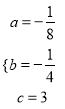： ，∴抛物线的表达式为；

（2）∵C（0，3），∴可设直线AC解析式为，把A点坐标代入可得0=﹣6k+3，解得k=，∴直线AC解析式为，设P点坐标为（x，0）（x＜0），则Q点坐标为（x， ），∴PQ=，PO=﹣x，∴S=PQPO== =，∴△CPQ的面积S的最大值为；

（3）当y=0时， ，解得x=﹣6或x=4，∴B点坐标为（4，0），∴BC==5，∵∠CDB=∠DCB，∴BD=BC=5，∴OD=BD﹣OB=5﹣4=1，∴D点坐标为（﹣1，0），∴D为AB中点，如图，连接DN，则DN=DM，∠NDC=∠MDC，∴∠NDC=∠DCB，∴DN∥BC，∵D是AB中点，∴N是AC中点，∴DN是△ABC的中位线，又DN=DM=BC=，∴OM=DM﹣OD==，∴点M坐标为（，0）．