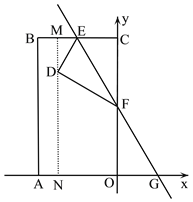
【题目】如图，矩形OABC在平面直角坐标系内（O为坐标原点），点A在x轴上，点C在y轴上，点B的坐标为（﹣4，﹣4），点E是BC的中点，现将矩形折叠，折痕为EF，点F为折痕与y轴的交点，EF交x轴于G且使∠CEF=60°．

（1）求证：△EFC≌△GFO；

（2）求点D的坐标；

（3）若点P（x，y）是线段EG上的一点，设△PAF的面积为s，求s与x的函数关系式并写出x的取值范围．

参考答案：

【答案】（1）证明见解析；（2）S=x

【解析】（1）先从B的坐标表示BC和OC的长，从点E为中点表示EC的长，根据60度的正切值得CF的长，依次可得OG、OF的长，根据两边及其夹角对应相等的两三角形全等得结论；

（2）如图2，构建矩形MNOC，分别计算DM、DN和MC的长，即可以表示D 坐标；

（3）分析两种情况讨论：①当-2≤x<0时P在线段EF上，如图3，②当0<x≤2时，P在线段FG上，如图4，利用面积差可以表示s与x的关系式.

解：（1）∵四边形ABCD是矩形，B（-4， ），

∴∠BCO=90°，BC=4，CO=，

∵点E是BC的中点，

∴EC=BC=2

∵∠CEF=60°

∴∠EFC=30°

∴EF=2

∴CF=，

∴OF=，

∴CF=OF=，

∵∠BCO=∠COG=90°，∠EFC=∠GFO，

∴△EFC≌△GFO ，

（2）解：过作DM⊥BC于M，延长MD交x轴于N，

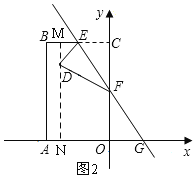
∵四边形MNOC是矩形

∴MN=CO=，

∵折痕为EF∴△EFC≌△EDF，

∴DE=CE=2，∠DEF=∠CEF=60°，

∴∠MED=60°∴∠MDE=30°，

∴ME=1，

∴DM=，

∴MC=2+1=3，DN=，

∴D坐标是（-3， ），

（3）∵EC=2，CF=OF=

∴F（0， ），E（-2， ）

设直线EF的解析式为y=kx+b，则，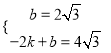

解得：b=，k=，

∴直线EF的解析式为y=x+，

∴△EFC≌△GFO，，

∴OG=EC=2AG=4+2=6，

当-2≤x<0时，

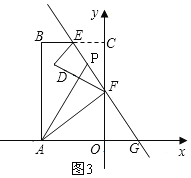
∵S△PAF=S△PAG-S△FAG，

∴s=，

==3（x+）-=x，

∴S=x ，

当0<x≤2时，

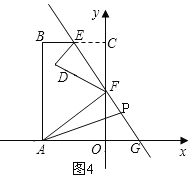
S△PAF=S△FAG-S△PAG，

∴s= ，

=x，

∴

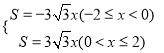
“点睛”本题是四边形的综合题，考查了矩形的性质、折叠的性质、三角形全等的性质和判定，特殊角的三角函数值。直角三角形30度的性质、三角形面积.且利用分类讨论的思想解决第三问的面积问题.

关闭