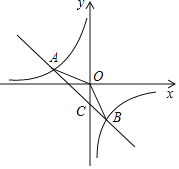
【题目】如图，在平面直角坐标系xOy中，一次函数y1＝ax+b（a，b为常数，且a≠0）与反比例函数y2＝（m为常数，且n≠0）的图象交于点A（﹣3，1）、B（1，n）．

（1）求反比例函数和一次函数的解析式；

（2）连结0A、OB，求△AOB的面积；

（3）直接写出当y1＜y2＜0时，自变量x的取值范围．

【答案】（1）反比例函数解析式为y2＝﹣；一次函数解析式为y1＝﹣x﹣2；（2）4；（3）x＞1

【解析】

(1)利用待定系数法，把A点坐标代入反比例函数的解析式，即可得到反比例函数的解析式；把A、B两点代入一次函数解析式中，即可求得一次函数的解析式；

(2)先求解C点的坐标，利用S△AOB＝S△AOC+S△COB即可求解；

(3)观察函数图像，即可得到答案；

解：（1）∵A（﹣3，1），

∴将A坐标代入反比例函数解析式y2＝中，得m＝﹣3，

∴反比例函数解析式为y2＝﹣；

将B（1，n）代入y＝﹣，得n＝﹣3，

∴B坐标（1，﹣3），

将A与B坐标代入一次函数解析式中，得，

解得a＝﹣1，b＝﹣2，

∴一次函数解析式为y1＝﹣x﹣2；

（2）设直线AB与y轴交于点C，

令x＝0，得y＝﹣2，

∴点C坐标（0，﹣2），

∴S△AOB＝S△AOC+S△COB＝×2×3+×1＝4；

（3）由图象可得，当x＞1时，反比例函数的图象再一次函数的上方，且反比例函数和一次函数的图象均在x轴的下方，

故当y1＜y2＜0时，自变量x的取值范围x＞1．

关闭