搜索
【题目】下列命题中真命题的个数是（ ）
①平面内，过一点有且只有一条直线与已知直线平行；②
这5个数中有2个是无理数；③若
，则点P(-m，5)在第一象限；④
的算术平方根是4；⑤经过一点有且只有一条直线与已知直线垂直；⑥同旁内角互补．
A.2B.3C.4D.5
参考答案：
【答案】A
【解析】
根据平行、垂直、无理数、坐标系、算术平方根和同旁内角分别判断即可．
解：①平面内，过直线外一点有且只有一条直线与已知直线平行，故本题说法错误；
②
这5个数中只有
这2个是无理数，说法正确；
③若
，则点P(-m，5)在第一象限，说法正确；
④
的算术平方根是2，故本题说法错误；
⑤在同一平面内，经过一点有且只有一条直线与已知直线垂直，故本题说法错误；
⑥两直线平行，同旁内角互补，故本题说法错误；
故只有2个是真命题；
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（10分）某体育用品专卖店销售7个篮球和9个排球的总利润为355元，销售10个篮球和20个排球的总利润为650元．
（1）求每个篮球和每个排球的销售利润；
（2）已知每个篮球的进价为200元，每个排球的进价为160元，若该专卖店计划用不超过17400元购进篮球和排球共100个，且要求篮球数量不少于排球数量的一半，请你为专卖店设计符合要求的进货方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在正方形ABCD外取一点E，连接AE，BE，DE，过点A作AE的垂线交DE于点P．若AE=AP=1，PB=
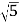．下列结论：①△APD≌△AEB；②点B到直线AE的距离为
；③EB⊥ED；④S△APD+S△APB=1+
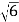．其中正确结论的序号是（ ）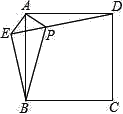
A. ①②③ B. ①②④ C. ②③④ D. ①③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题情境：如图1，
，
，
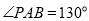．求 
度数．小明的思路是：如图2，过
作 
，通过平行线性质，可得 
．
问题迁移：
（1）如图3，
，点 在射线 
上运动，当点 在 
、 
两点之间运动时，
，
．
、 
、 
之间有何数量关系?请说明理由；（2）在（1）的条件下，如果点
在 、 两点外侧运动时（点 与点 、 、 
三点不重合），请你直接写出 、 、 间的数量关系． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A（a﹣2b，2﹣4ab）在抛物线y=x2+4x+10上，则点A关于抛物线对称轴的对称点坐标为（ ）
A.（﹣3，7）
B.（﹣1，7）
C.（﹣4，10）
D.（0，10） -
科目： 来源： 题型：
查看答案和解析>>【题目】请从以下两个小题中任选一题作答，若多选，则按所选的第一题计分．
A．正五边形的一个外角的度数是 ．
B．比较大小：2tan71°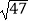
（填“＞”、“=”或“＜”） -
科目： 来源： 题型：
查看答案和解析>>【题目】小丽的家和学校在一条笔直的马路旁，某天小丽沿着这条马路去上学，她先从家步行到公交站台甲，再乘车到公交站台乙下车，最后步行到学校(在整个过程中小丽步行的速度不变)，图中的折线ABCDE表示小丽和学校之间的距离y(米)与她离家的时间x(分)之间的函数关系．
(1)求小丽步行的速度及学校与公交站台乙之间的距离；
(2)当8≤x≤15时，求y与x之间的函数解析式．
相关试题
