【题目】如图，已知的直径，是的弦，过点作的切线交的延长线于点，过点作，垂足为，与交于点，设，的度数分别是，，且．

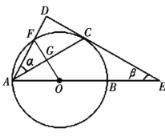
（1）用含的代数式表示；

（2）连结交于点，若，求的长．

【答案】（1）；（2）

【解析】

（1）连接OC，根据切线的性质得到OC⊥DE，可以证明AD∥OC，根据平行线的性质可得，则根据等腰三角形的性质可得，利用，化简计算即可得到答案；
（2）连接CF，根据，可得，利用中垂线和等腰三角形的性质可证四边形是平行四边形，得到△AOF为等边三角形，由并可得四边形是菱形，可证是等边三角形，有∠FAO=60°，再根据弧长公式计算即可．

解：（1）如图示，连结，

∵是的切线，∴．

又，∴，

∴，

∴．

∵，

∴．∴．

∵，

∴．

∴，即．

（2）如图示，连结，

∵，，

∴，

∴，

∴，

∴，

∵，

∴四边形是平行四边形，

∵，

∴四边形是菱形，

∴，

∴是等边三角形，

∴，

∴，

∵，

∴的长．

关闭