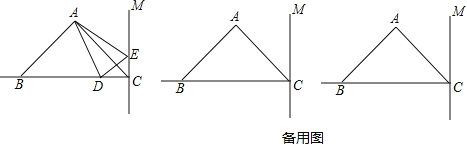
【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=10cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒2厘米的速度运动,连接AD、AE,设运动时间为t秒.
(1)求AB的长;(2)当t为多少时,△ABD的面积为15cm2?
(3)当t为多少时,△ABD≌△ACE,并简要说明理由.(请在备用图中画出具体图形)
参考答案:
【答案】(1)5![]() ;(2)2或8; (3)2或10.
;(2)2或8; (3)2或10.
【解析】试题分析:(1)运用勾股定理直接求出;(2)首先求出△ABD中BD边上的高,然后根据面积公式列出方程,求出BD的值,分两种情况分别求出t的值;(3)假设△ABD≌△ACE,根据全等三角形的对应边相等得出BD=CE,分别用含t的代数式表示CE和BD,得到关于t的方程,从而求出t的值.
试题解析:(1)∵在△ABC中,AB=AC,∠BAC=90°,
∴2AB2=BC2,
∴AB=![]() =5
=5![]() cm;
cm;
(2)过A作AF⊥BC交BC于点F,
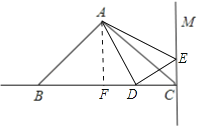
则AF=![]() BC=5cm,
BC=5cm,
∵S△ABD=15cm2,
∴AF×BD=30,
∴BD=6cm.
若D在B点右侧,则CD=4cm,t=2s;
若D在B点左侧,则CD=16cm,t=8s.
(3)动点E从点C沿射线CM方向运动2秒或当动点E从点C沿射线CM的反向延长线方向运动6秒时,△ABD≌△ACE.
理由如下:(说理过程简要说明即可)
①当E在射线CM上时,D必在CB上,则需BD=CE.
∵CE=2t,BD=10﹣3t
∴2t=10﹣3t
∴t=2
证明:在△ABD和△ACE中,
∵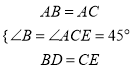 ,
,
∴△ABD≌△ACE(SAS).
②当E在CM的反向延长线上时,D必在CB延长线上,则需BD=CE.
∵CE=2t,BD=3t﹣10,
∴2t=3t﹣10,
∴t=10
证明:在△ABD和△ACE中,
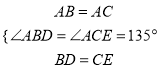
∴△ABD≌△ACE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4x2﹣12xy+9y2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x1,x2是方程x2+3x﹣1=0的两个根,则x1+x2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数x,y满足|x﹣4|+(y﹣8)2=0,则以x,y的值为两边长的等腰三角形的周长是( )
A.20或16B.20C.16D.以上答案均不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016贵州省毕节市第10题)如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数
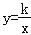 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )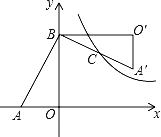
A.3 B.4 C.6 D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+2x﹣1=0的实数根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.没有实数根
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的多项式x2﹣kx+9是一个完全平方式,那么k= .
相关试题

