【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
参考答案:
【答案】(1)通过证明OM⊥AE即可证明AE与⊙O相切。
(2)半径为![]()
【解析】试题分析:(1)连接OM.根据OB=OM,得∠OMB=∠OBM,结合BM平分∠ABC交AE于点M,得∠OBM=∠EBM,则OM∥BE;根据等腰三角形三线合一的性质,得AE⊥BC,则OM⊥AE,从而证明结论;(2)设圆的半径是r.根据等腰三角形三线合一的性质,得BE=CE=2,再根据解直角三角形的知识求得AB=6,则OA=6-r,从而根据平行线分线段成比例定理求解;
试题解析:
(1) 连接OM,则OM=OB,如图所示:
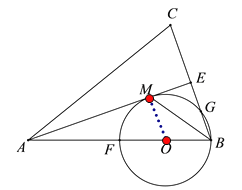
∴∠OBM=∠OMB
∵BM平分∠ABC
∴∠OBM=∠EBM
∴∠OMB=∠EBM
∴OM∥BE
∴∠AMO=∠AEB
而在⊿ABC中,AB=AC,AE是角平分线
∴AE⊥BC
∴∠AMO=∠AEB=90°
∴AE与⊙O相切.
(2) 在⊿ABC中,AB=AC,AE是角平分线
∴BE=![]() BC=2,∠ABC=∠ACB
BC=2,∠ABC=∠ACB
∴在Rt⊿ABC中cos∠ABC=cos∠ACB=![]() =
=![]()
∴AB=6
设⊙O的半径为r,则AO=6-r
∵OM∥BC
∴△AOM∽△ABE
∴![]() =
=![]()
即 ![]() =
=![]()
∴r=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣12+(﹣2)×3﹣1÷(﹣0.2)﹣|﹣4|
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
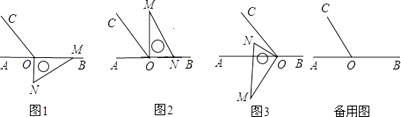
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简3x﹣2(x﹣3y)的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示:20140000000应记为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2b+2ab2+b3=
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是一名学生所做的4道练习题:①﹣22=4②a3+a3=a6③4m﹣4=
 ④(xy2)3=x3y6 , 他做对的个数( )
④(xy2)3=x3y6 , 他做对的个数( )
A.1
B.2
C.3
D.4
相关试题

