【题目】在平面直角坐标系中,点A、B的坐标分别为(a,0),(0,b),其中a,b满足 ![]() +|2a﹣5b﹣30|=0.将点B向右平移26个单位长度得到点C,如图①所示.
+|2a﹣5b﹣30|=0.将点B向右平移26个单位长度得到点C,如图①所示.
(1)求点A,B,C的坐标;
(2)点M,N分别为线段BC,OA上的两个动点,点M从点C向左以1.5个单位长度/秒运动,同时点N从点O向点A以2个单位长度/秒运动,如图②所示,设运动时间为t秒(0<t<15).
①当CM<AN时,求t的取值范围;
②是否存在一段时间,使得S四边形MNOB>2S四边形MNAC?若存在,求出t的取值范围;若不存在,说明理由.
参考答案:
【答案】
(1)解:∵ ![]() +|2a﹣5b﹣30=0,且
+|2a﹣5b﹣30=0,且 ![]() ≥0,|2a﹣5b﹣30|≥0,
≥0,|2a﹣5b﹣30|≥0,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴A(30,0),B(0,6),
又∵点C是由点B向右平移26个单位长度得到,
∴C(26,6)
(2)解:①由(1)可知:OA=30,
∵点M从点C向右以1.5个单位长度/秒运动,点N从点O向点A以2个单位长度/秒运动,
∴CM=1.5t,ON=2t,
∴AN=30﹣2t
∵CM<AN,
∴1.5t<30﹣2t,解得t< ![]() ,而0<t<15,
,而0<t<15,
∴0<t< ![]() ;
;
②由题意可知CM=1.5t,ON=2t,
∴BM=BC﹣CM=26﹣1.5t,AN=30﹣2t,
又B(0,6),
∴OB=6,
∴S四边形MNOB= ![]() OB(BM+ON)=3(26﹣1.5t+2t)=3(26+0.5t),S四边形MNAC=
OB(BM+ON)=3(26﹣1.5t+2t)=3(26+0.5t),S四边形MNAC= ![]() OB(AN+CM)=3(30﹣2t+1.5t)=3(30﹣0.5t),
OB(AN+CM)=3(30﹣2t+1.5t)=3(30﹣0.5t),
当S四边形MNOB>2S四边形MNAC时,则有3(26+0.5t)>2×3(30﹣0.5t),解得t> ![]() >15,
>15,
∴不存在使S四边形MNOB>2S四边形MNAC的时间段.
【解析】(1)由条件可求得a、b的值,则可求得A、B两点的坐标,再由平移可求得C点坐标;(2)①用t可分别表示出CM和AN,由条件可得到关于t不等式,可求得t的取值范围;②用t表示出四边形MNOB和四边形MNAC的面积,由条件得到t的不等式,再结合t的取值范围进行判定即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A.(2,5)
B.(5,2)
C.(4, )
)
D.( ,4)
,4) -
科目: 来源: 题型:
查看答案和解析>>【题目】点P是直线l外一点,点A,B,C,D是直线l上的点,连接PA,PB,PC,PD.其中只有PA与l垂直,若PA=7,PB=8,PC=10,PD=14,则点P到直线l的距离是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.

(1)若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1 , 再将点P1绕原点旋转90°得到点P2 , 则点P2的坐标是( )
A.(3,﹣3)
B.(﹣3,3)
C.(3,3)或(﹣3,﹣3)
D.(3,﹣3)或(﹣3,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
(1)AE的长等于________;
(2)若点P在线段AC上,点Q在线段BC上,且满足AP = PQ = QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明)________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )
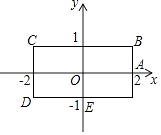
A.(1,﹣1)
B.(2,0)
C.(﹣1,1)
D.(﹣1,﹣1)
相关试题

