Question

【题目】在△ABC中，AB=AC．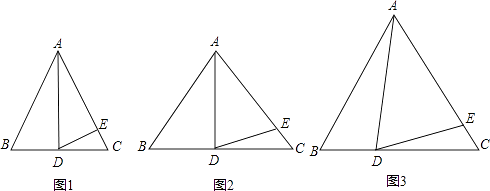

（1）如图1，如果∠BAD=30°，AD是BC上的高，AD=AE，则∠EDC=
（2）如图2，如果∠BAD=40°，AD是BC上的高，AD=AE，则∠EDC=
（3）思考：通过以上两题，你发现∠BAD与∠EDC之间有什么关系？请用式子表示：
（4）如图3，如果AD不是BC上的高，AD=AE，是否仍有上述关系？如有，请你写出来，并说明理由．

Answer 1

【答案】
（1）15°
（2）20°
（3）∠EDC= ∠BAD
（4）解：仍成立，理由如下

∵AD=AE，∴∠ADE=∠AED，

∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=（∠EDC+∠C）+∠EDC

=2∠EDC+∠C

又∵AB=AC，

∴∠B=∠C

∴∠BAD=2∠EDC．

故分别填15°，20°，∠EDC= ∠BAD

【解析】（1）根据等腰三角形的性质三线合一和∠BAD=30°，得到△ABC是等边三角形，由AD=AE和三角形的一个外角等于和它不相邻的两个内角之和
，求出∠EDC的度数；（2）由∠BAD=40°，AD是BC上的高，AD=AE，根据三角形内角和定理和三线合一，求出∠EDC的度数；（3）根据等腰三角形的性质和三角形内角和定理，得出结论∠EDC=∠BAD.