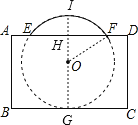
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为 .

参考答案:
【答案】5.
【解析】
试题分析:首先由题意,⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧![]() 于点H、I,再连接OF,易求得FH的长,然后设求半径为r,则OH=8﹣r,然后在Rt△OFH中,r2﹣(16﹣r)2=82,解此方程即可求得答案.
于点H、I,再连接OF,易求得FH的长,然后设求半径为r,则OH=8﹣r,然后在Rt△OFH中,r2﹣(16﹣r)2=82,解此方程即可求得答案.
解:由题意,⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧![]() 于点H、I,再连接OF,
于点H、I,再连接OF,
在矩形ABCD中,AD∥BC,而IG⊥BC,
∴IG⊥AD,
∴在⊙O中,FH=![]() EF=4,
EF=4,
设求半径为r,则OH=8﹣r,
在Rt△OFH中,r2﹣(8﹣r)2=42,
解得r=5,
故答案为:5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠C=
 ,∠EAC+∠FBC=
,∠EAC+∠FBC=
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则
 与
与 有何关系?并说明理由.
有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与
 、
、 的关系是 .(用
的关系是 .(用 、
、 表示)
表示)
(3)如图③,若
 ≥
≥ ,∠EAC与∠FBC的平分线相交于
,∠EAC与∠FBC的平分线相交于 ,
,  ;依此类推,则
;依此类推,则 = (用
= (用 、
、 表示)
表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )

A.SAS B.ASA C.AAS D.SSS
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=
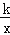 (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .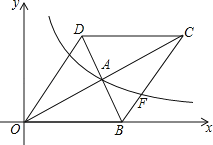
-
科目: 来源: 题型:
查看答案和解析>>【题目】长度分别为2,7,x的三条线段能组成一个三角形,x的值可以是( )
A. 4 B. 5 C. 6 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=2是方程k(x-3)=1的解,则k=____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+2(m-3)x+16是完全平方式,则m表示的数是( )
A. 3 B. -5 C. 7 D. -1或7
相关试题

