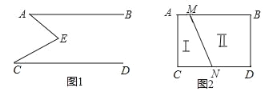
【题目】如图1,AB∥CD,点E是直线AB、CD之间的一点,连接EA、EC.
(1)探究猜想:
①若∠A=20°,∠C=50°,则∠AEC= .
②若∠A=25°,∠C=40°,则∠AEC= .
③猜想图1中∠EAB、∠ECD、∠AEC的关系,并证明你的结论(提示:作EF∥AB).
(2)拓展应用:
如图2,AB∥CD,线段MN把ABCD这个封闭区域分为I、Ⅱ两部分(不含边界),点E是位于这两个区域内的任意一点,请直接写出∠EMB、∠END、∠MEN的关系.
参考答案:
【答案】(1)70°;65°;猜想:∠AEC=∠EAB+∠ECD.(2)当点E位于区域Ⅰ时,∠EMB+∠END+∠MEN=360°;当点E位于区域Ⅱ时,∠EMB+∠END=∠MEN.
【解析】
(1)①过点E作EF∥AB,再由平行线的性质即可得出结论;②、③根据①的过程可得出结论;
(2)根据题意画出图形,再根据平行线的性质即可得出∠EMB、∠END、∠MEN的关系.
本题考查的是平行线的性质,根据题意画出图形,利用数形结合求解是解答此题的关键.
解:(1)①如图1,过点E作EF∥AB,
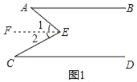
∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=20°,∠C=50°,
∴∠1=∠A=20°,∠2=∠C=50°,
∴∠AEC=∠1+∠2=70°;
故答案为:70°;
②同理可得,∴∠AEC=∠1+∠2=65°;
故答案为:65°;
③猜想:∠AEC=∠EAB+∠ECD.
理由:如图1,过点E作EF∥CD,
∵AB∥DC
∴EF∥AB(平行于同一条直线的两直线平行),
∴∠1=∠EAB,∠2=∠ECD(两直线平行,内错角相等),
∴∠AEC=∠1+∠2=∠EAB+∠ECD(等量代换).
(2)当点E位于区域Ⅰ时,∠EMB+∠END+∠MEN=360°,
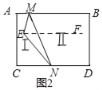
理由:过E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BME+∠MEF=180°,∠DNE+∠NEF=180°,
∴∠EMB+∠END+∠MEN=360°;
当点E位于区域Ⅱ时,∠EMB+∠END=∠MEN,
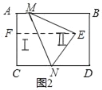
理由:过E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BMN=∠FEM,∠DNE=∠FEN,
∴∠EMB+∠END=∠MEF+∠NEF=∠MEN.
-
科目: 来源: 题型:
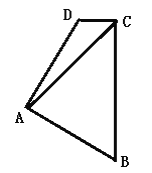
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=900,连结AC,若AC=10,则四边形ABCD的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.

(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
已知某中学计划租用A、B两种型号的客车共10辆,同时送七年级师生到沙家参加社会实践活动,已知该中学租车的总费用不超过5600元.
(1)求最多能租用多少辆A型号客车?
(2)若七年级的师生共有380人,请写出所有可能的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明用12元买软面笔记本,小丽用21元买硬面笔记本.
(1)已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗?
(2)已知每本硬面笔记本比软面笔记本贵a元,是否存在正整数a,使得每本硬面笔记本、软面笔记本的价格都是正整数,并且小明和小丽能买到相同数量的笔记本?若存在,求出a的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 .
.
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在10×10的网格中,有一格点三角形ABC.(说明:顶点都在网格线交点处的三角形叫做格点三角形)

(1)将△ABC绕点C旋转180°,得到△A′B′C,请直接画出旋转后的△A′B′C.(友情提醒:别忘了标上相应的字母!)
(2)在网格中以AB为一边作格点△ABD(顶点在小正方形的顶点处的三角形称为格点三角形),使它的面积是△ABC的2倍,则点D的个数有个.
相关试题

