【题目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),分别以AB、BC为边作等边三角形ABE和等边三角形BCD,连结CE,如图1所示.

(1)直接写出∠ABD的大小(用含α的式子表示);
(2)判断DC与CE的位置关系,并加以证明;
(3)在(2)的条件下,连结DE,如图2,若∠DEC=45°,求α的值.
参考答案:
【答案】(1)∠ABD=30°﹣![]() ∠α;(2)DC与CE垂直;见解析(3)∠α=30°.
∠α;(2)DC与CE垂直;见解析(3)∠α=30°.
【解析】
试题分析:(1)根据等腰三角形的性质得到∠ABC=∠ACB=![]() =90°﹣
=90°﹣![]() ∠α,根据角的和差即可得到结论;
∠α,根据角的和差即可得到结论;
(2)连接AD;根据已知条件得到∠ABD=∠EBC,推出△ABD≌△EBC,根据全等三角形的性质得到∠ADB=∠ECB,证得△ABD≌△ACD,由全等三角形的性质得到∠BAD=∠CAD=![]() ∠α,根据三角形的内角和得到∠BDA=180°﹣∠ABD﹣∠BAD=180°﹣(30°﹣
∠α,根据三角形的内角和得到∠BDA=180°﹣∠ABD﹣∠BAD=180°﹣(30°﹣![]() ∠α )﹣
∠α )﹣![]() ∠α=150°,求得∠BCE=150°,即可得到结论.
∠α=150°,求得∠BCE=150°,即可得到结论.
(3)根据已知条件得到△DEC为等腰三角形,根据等腰直角三角形的性质得到DC=DE=BC,根据三角形的内角和得到∠EBC=15°,即可得到结论.
解:(1)∵AB=AC,∠A=∠α,
∴∠ABC=∠ACB=![]()
=90°﹣![]() ∠α
∠α
∴∠ABD=∠ABC﹣∠ABE
=90°﹣![]() ∠α﹣60°
∠α﹣60°
=30°﹣![]() ∠α;
∠α;
(2)DC与CE垂直;
连接AD;
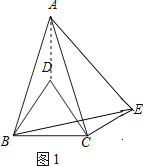
∵∠ABE=∠DBC=60°,
∴∠ABE﹣∠DBE=∠DBC﹣∠DBE,
即∠ABD=∠EBC,
在△ABD和△EBC中,
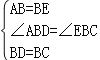 ,
,
∴△ABD≌△EBC,
∴∠ADB=∠ECB,
在△ABD和△ACD中,
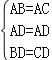 ,
,
∴△ABD≌△ACD,
∴∠BAD=∠CAD=![]() ∠α,
∠α,
∴∠BDA=180°﹣∠ABD﹣∠BAD=180°﹣(30°﹣![]() ∠α )﹣
∠α )﹣![]() ∠α=150°,
∠α=150°,
∴∠BCE=150°,
∵∠BCD=60°,
∴∠DCE=90°,
即DC与CE垂直;
(3)∵∠DCE=90°,
又∵∠DEC=45°,
∴△DEC为等腰三角形,
∴DC=DE=BC,
∵∠BCE=150°,
∴∠EBC=15°,
∵∠EBC=30°﹣![]() ∠α=15°,
∠α=15°,
∴∠α=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个布袋中装有2个红球和2个篮球,它们除颜色外其他都相同.
(1)搅匀后从中摸出一个球记下颜色,不放回继续再摸第二个球,求两次都摸到红球的概率;
(2)在这4个球中加入x个用一颜色的红球或篮球后,进行如下试验,搅匀后随机摸出1个球记下颜色,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到红球的概率稳定在0.80,请推算加入的是哪种颜色的球以及x的值大约是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象经过A(1,0),B(3,0),C(0,﹣3)
(1)求此二次函数的解析式以及顶点D的坐标;
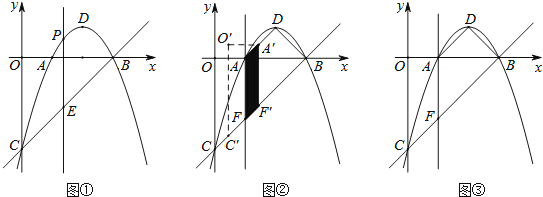
(2)如图①,过此二次函数抛物线图象上一动点P(m,n)(0<m<3)作y轴平行线,交直线BC于点E,是否存在一点P,使线段PE的长最大?若存在,求出PE长的最大值;若不存在,说明理由.
(3)如图②,过点A作y轴的平行线交直线BC于点F,连接DA、DB、四边形OAFC沿射线CB方向运动,速度为每秒1个单位长度,运动时间为t秒,当点C与点F重合时立即停止运动,求运动过程中四边形OAFC与四边形ADBF重叠部分面积S的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴交于点O、M.对称轴为直线x=2,以OM为直径作圆A,以OM的长为边长作菱形ABCD,且点B、C在第四象限,点C在抛物线对称轴上,点D在y轴负半轴上;
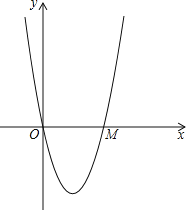
(1)求证:4a+b=0;
(2)若圆A与线段AB的交点为E,试判断直线DE与圆A的位置关系,并说明你的理由;
(3)若抛物线顶点P在菱形ABCD的内部且∠OPM为锐角时,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查显示,截止2015年底某市汽车拥有量为16.9万辆.己知2013年底该市汽车拥有量为10万辆,设2013年底至2015年底该市汽车拥有量的平均增长率为x,根据题意列方程得( )
A.10(1+x)2=16.9 B.10(1+2x)=16.9 C.10(1﹣x)2=16.9 D.10(1﹣2x)=16.9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点A在y轴正半轴上,点B的坐标为(0,﹣3),反比例函数y=﹣
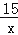 的图象经过点C.
的图象经过点C.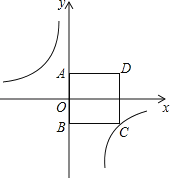
(1)求点C的坐标;
(2)若点P是反比例函数图象上的一点且S△PAD=S正方形ABCD;求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
相关试题

