【题目】试找出如图所示的每个正多边形的对称轴的条数,并填入表格中.
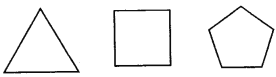
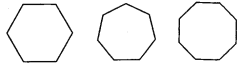
正多边形的边数 | 3 | 4 | 5 | 6 | 7 | 8 |
对称轴的条数 |
根据上表,请就一个正n边形对称轴的条数作一猜想.
参考答案:
【答案】3,4,5,6,7,8 n
【解析】
正多变形都是轴对称图形,其对称轴为任意边上的垂直平分线.
正三角形每条边上的垂直平分线都是对称轴,有3条边,故有3条对称轴;
正四边形每条边上的垂直平分线都是对称轴,有4条边,故有4条对称轴;
正五边形每条边上的垂直平分线都是对称轴,有5条边,故有5条对称轴;
正六边形每条边上的垂直平分线都是对称轴,有6条边,故有6条对称轴;
正七边形每条边上的垂直平分线都是对称轴,有7条边,故有7条对称轴;
正八边形每条边上的垂直平分线都是对称轴,有8条边,故有8条对称轴;
由以上规律可得:正n边形,就有n条对称轴.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
组别
平均分
中位数
方差
合格率
优秀率
甲组
6.7
3.41
90%
20%
乙组
7.5
1.69
80%
10%
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.

(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC= ?请说明理由.
?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.

(1)请判断:FG与CE的数量关系是 , 位置关系是;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断. -
科目: 来源: 题型:
查看答案和解析>>【题目】公园内两条小河MO、NO在O处汇合,如图所示,两河形成的平地上要建一个小百货店,使小百货店到两岸边距离相等,到两河交汇处距离300米,百货店的位置该怎样确定?请你按10000:1的比例,在图中确定百货店的位置,并估算一下,它到河边的距离.
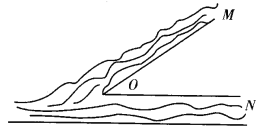
-
科目: 来源: 题型:
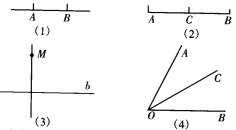
查看答案和解析>>【题目】看图填空:
(1)过点________和点_______作直线;
(2)延长线段________到_________,且使________=_________.
(3)过点_________作直线_______的垂线;
(4)作射线_______,使_____平分∠________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
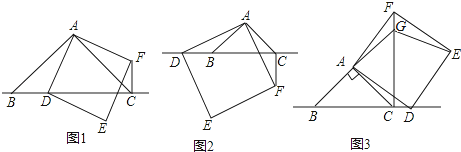
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2 ,CD=
,CD=  BC,请求出GE的长.
BC,请求出GE的长.
相关试题

