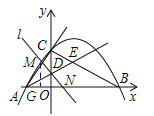
【题目】如图,已知抛物线![]() 与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
(1)直接写出a的值、点A的坐标及抛物线的对称轴;
(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;
(3)证明:当直线l绕点D旋转时,![]() 均为定值,并求出该定值.
均为定值,并求出该定值.

参考答案:
【答案】(1)a=![]() ,A(﹣
,A(﹣![]() ,0),抛物线的对称轴为x=
,0),抛物线的对称轴为x=![]() ;(2)点P的坐标为(
;(2)点P的坐标为(![]() ,2)或(
,2)或(![]() ,0)或(
,0)或(![]() ,﹣4);(3)
,﹣4);(3)![]() .
.
【解析】
试题分析:(1)由点C的坐标为(0,3),可知﹣9a=3,故此可求得a的值,然后令y=0得到关于x的方程,解关于x的方程可得到点A和点B的坐标,最后利用抛物线的对称性可确定出抛物线的对称轴;
(2)利用特殊锐角三角函数值可求得∠CAO=60°,依据AE为∠BAC的角平分线可求得∠DAO=30°,然后利用特殊锐角三角函数值可求得OD=1,则可得到点D的坐标.设点P的坐标为(![]() ,a).依据两点的距离公式可求得AD、AP、DP的长,然后分为AD=PA、AD=DP、AP=DP三种情况列方程求解即可;
,a).依据两点的距离公式可求得AD、AP、DP的长,然后分为AD=PA、AD=DP、AP=DP三种情况列方程求解即可;
(3)设直线MN的解析式为y=kx+1,接下来求得点M和点N的横坐标,于是可得到AN的长,然后利用特殊锐角三角函数值可求得AM的长,最后将AM和AN的长代入化简即可.
试题解析:(1)∵C(0,3),∴﹣9a=3,解得:a=![]() .
.
令y=0得:![]() ,∵a≠0,∴
,∵a≠0,∴![]() ,解得:x=﹣
,解得:x=﹣![]() 或x=
或x=![]() ,∴点A的坐标为(﹣
,∴点A的坐标为(﹣![]() ,0),B(
,0),B(![]() ,0),∴抛物线的对称轴为x=
,0),∴抛物线的对称轴为x=![]() .
.
(2)∵OA=![]() ,OC=3,∴tan∠CAO=
,OC=3,∴tan∠CAO=![]() ,∴∠CAO=60°.
,∴∠CAO=60°.
∵AE为∠BAC的平分线,∴∠DAO=30°,∴DO=![]() AO=1,∴点D的坐标为(0,1).
AO=1,∴点D的坐标为(0,1).
设点P的坐标为(![]() ,a).
,a).
依据两点间的距离公式可知:AD2=4,AP2=12+a2,DP2=3+(a﹣1)2.
当AD=PA时,4=12+a2,方程无解.
当AD=DP时,4=3+(a﹣1)2,解得a=2或a=0,∴点P的坐标为(![]() ,2)或(
,2)或(![]() ,0).
,0).
当AP=DP时,12+a2=3+(a﹣1)2,解得a=﹣4,∴点P的坐标为(![]() ,﹣4).
,﹣4).
综上所述,点P的坐标为(![]() ,2)或(
,2)或(![]() ,0)或(
,0)或(![]() ,﹣4).
,﹣4).
(3)设直线AC的解析式为y=mx+3,将点A的坐标代入得:![]() ,解得:m=
,解得:m=![]() ,∴直线AC的解析式为
,∴直线AC的解析式为![]() .
.
设直线MN的解析式为y=kx+1.
把y=0代入y=kx+1得:kx+1=0,解得:x=![]() ,∴点N的坐标为(
,∴点N的坐标为(![]() ,0),∴AN=
,0),∴AN=![]() =
=![]() .
.
将![]() 与y=kx+1联立解得:x=
与y=kx+1联立解得:x=![]() ,∴点M的横坐标为
,∴点M的横坐标为![]() .
.
过点M作MG⊥x轴,垂足为G.则AG=![]() .
.
∵∠MAG=60°,∠AGM=90°,∴AM=2AG=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程3x﹣2m=6的解是x=m,则m的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(﹣2,1)与点B关于原点对称,则点B的坐标为( )
A.(﹣2,1)
B.(2,﹣1)
C.(2,1)
D.(﹣2,﹣1) -
科目: 来源: 题型:
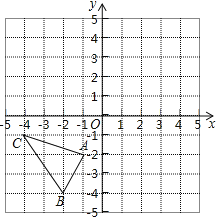
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)把△ABC向上平移3个单位后得到△A1B1C1,请画出△A1B1C1并写出点B1的坐标;
(2)已知点A与点A2(2,1)关于直线l成轴对称,请画出直线l及△ABC关于直线l对称的△A2B2C2,并直接写出直线l的函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】湘西土家族苗族自治州6月2日至6月8日最高气温(℃)统计如下表:
日期
2日
3日
4日
5日
6日
7日
8日
最高气温℃
28
25
25
30
32
28
27
则这七天最高气温的中位数为( )
A.25℃
B.27℃
C.28℃
D.30℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】为调查广西北部湾四市市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:

(1)在这次调查中,一共调查了 名市民,扇形统计图中,C组对应的扇形圆心角是 °;
(2)请补全条形统计图;
(3)若甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种,则甲、乙两人恰好选择同一种交通工具上班的概率是多少?请用画树状图或列表法求解.
-
科目: 来源: 题型:
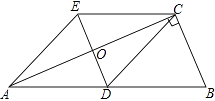
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE. 求证:四边形ADCE是菱形.
相关试题

