Question

【题目】如图，已知抛物线经过点A（2，0），B（3，3）及原点O，顶点为C．

（1）求抛物线的解析式；

（2）若点D在抛物线上，点E在抛物线的对称轴上，且以A，O，D，E为顶点的四边形是平行四边形，求点D的坐标；

（3）P是抛物线上第二象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P使得以点P，M，A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y=x2-2x；（2）点P的坐标为(-，)或（-3，15）．

【解析】

试题分析：（1）根据抛物线过A（2，0）及原点可设y=a（x-2）x，然后根据抛物线y=a（x-2）x过B（3，3），求出a的值即可；

（2）首先由A的坐标可求出OA的长，再根据四边形AODE是平行四边形，D在对称轴直线x=-1右侧，进而可求出D横坐标为：-1+2=1，代入抛物线解析式即可求出其横坐标；

（3）分△PMA∽△COB和△PMA∽△BOC表示出PM和AM，从而表示出点P的坐标，代入求得的抛物线的解析式即可求得t的值，从而确定点P的坐标．

试题解析：（1）根据抛物线过A（2，0）及原点，可设y=a（x-2）（x-0），

又∵抛物线y=a（x-2）x过B（3，3），

∴3（3-2）a=3，

∴a=1，

∴抛物线的解析式为y=（x-2）x=x2-2x；

（2）①若OA为对角线，则D点与C点重合，点D的坐标应为D（1，-1）；

②若OA为平行四边形的一边，则DE=OA，∵点E在抛物线的对称轴上，

∴点E横坐标为1，

∴点D的横坐标为3或-1，代入y=x2-2x得D（3，3）和D（-1，3），

综上点D坐标为（1，-1），（3，3），（-1，3）．

（3）∵点B（3，3）C（1，-1），

∴△BOC为直角三角形，∠COB=90°，且OC：OB=1：3，

①如图1，

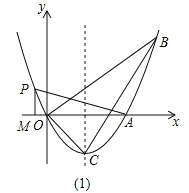
若△PMA∽△COB，设PM=t，则AM=3t，

∴点P（2-3t，t），

代入y=x2-2x得（2-3t）2-2（2-3t）=t，

解得t1=0（舍），t2=，

∴P(-，)；

②如图2，

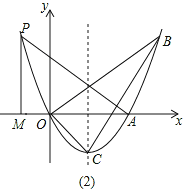
若△PMA∽△BOC，

设PM=3t，则AM=t，点P（2-t，3t），代入y=x2-2x得（2-t）2-2（2-t）=3t，

解得t1=0（舍），t2=5，

∴P（-3，15）

综上所述，点P的坐标为(-，)或（-3，15）．