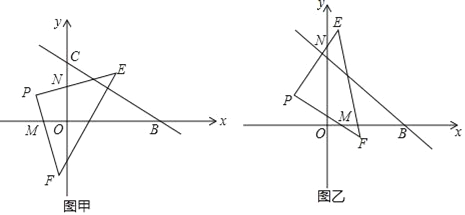
【题目】如图,在平面直角坐标系中,已知B(8,0),C(0,6),P(﹣3,3),现将一直角三角板EPF的直角顶点放在点P处,EP交y轴于N,FP交x轴于M,把△EPF绕点P旋转:
(1)如图甲,①求OM+ON的值;
②求BM﹣CN的值;
(2)如图乙,①求ON﹣OM的值;
②求BM+CN的值.
参考答案:
【答案】(1)6,8;(2)6,8.
【解析】试题分析:(1)如图甲中,①作PG⊥x轴于G,PH⊥y轴于H,得到矩形PGOH,根据矩形的性质和全等三角形的判定定理证明△NPH≌△MPG,得到NH=MG,根据图形的性质得到答案.②根据②BM-CN=OB+OM-(OC-ON)=OB-OC+OM+ON计算即可.
(2)如图乙中,①作PG⊥x轴于G,PH⊥y轴于H,由△NPH≌△MPG,推出NH=MG,推出ON-OM=(OH+HN)-(GM-OG)=OG+OH=6.
②根据BM+CN=(OB-OM)+(ON-OC)=OB-OC+ON-OM计算即可.
试题解析:(1)如图甲中,①作PG⊥x轴于G,PH⊥y轴于H,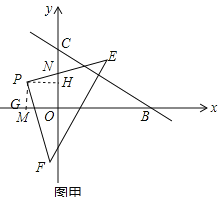
∵四边形PGOH为矩形,
∴∠HPG=90°,又∠EPF=90°,
∴∠NPH=∠MPG,
∵P(-3,3),
∴PH=PG=3,
在△NPH和△MPG中,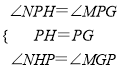 ,
,
∴△NPH≌△MPG,
∴NH=MG,
∴OM+ON=(OG-GM)+(HN+OH)=OG+OH=6.
②BM-CN=OB+OM-(OC-ON)=OB-OC+OM+ON=8-6+6=8.
(2)如图乙中,①作PG⊥x轴于G,PH⊥y轴于H,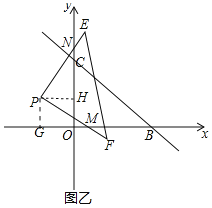
∵四边形PGOH为矩形,
∴∠HPG=90°,又∠EPF=90°,
∴∠NPH=∠MPG,
∵P(-3,3),
∴PH=PG=3,
在△NPH和△MPG中,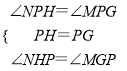 ,
,
∴△NPH≌△MPG,
∴NH=MG,
∴ON-OM=(OH+HN)-(GM-OG)=OG+OH=6.
②BM+CN=(OB-OM)+(ON-OC)=OB-OC+ON-OM=8-6+6=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y1=-x2+2向右平移1个单位得到的抛物线y2.回答下列问题:
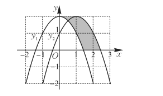
(1)抛物线y2的解析式是_____,顶点坐标为_____;
(2)阴影部分的面积_____;
(3)若再将抛物线y2绕原点O旋转180°得到抛物线y3,则抛物线y3的解析式为_____,开口方向_____,顶点坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从超市出发,向东走了2km,到达小刚家,继续向东走了3km到达小红家,又向西走了9km到达小英家,最后回到超市.
(1)请以超市为原点,以向东方向为正方向,用1个单位长度表示1km,画出数轴.并在数轴上表示出小刚家、小红家、小英家的位置;
(2)小英家距小刚家有多远?
(3)货车一共行驶了多少千米? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
(1)求二次函数的解析式;
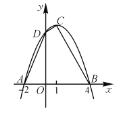
(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据2、1、0、-2、0、-1的中位数与众数分别是( )
A. 0和0B. -1和0C. 0和0D. 0和2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=a
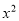 +bx的图象过点 (2,0),(-1,6).
+bx的图象过点 (2,0),(-1,6).(1)求二次函数的关系式;
(2)写出它的对称轴和顶点坐标;
(3)请说明x在什么范围内取值时,函数值y<0?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O1与⊙O2内切于点A,⊙O1的半径等于5,O1 O2=3,那么O2A的长等于( )
A. 2B. 3C. 8D. 2或8
相关试题

