【题目】如图,⊙M与x轴相交于A(2,0)、B(8,0),与y轴相切于点C,P是优弧AB上的一点,则tan∠APB为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解:如图,作MN⊥AB于N,连接PA、PB、MA、MB、MC. 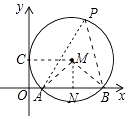
∵A(2,0),B(8,0),
∴OA=2,OB=8,AN=BN=3,
∵C是切点,
∴∠MCO=∠CON=∠MNO=90°,
∴四边形CONM是矩形,
∴CM=AM=ON=5,
在Rt ![]() AMN中,MN=
AMN中,MN= ![]() =4,
=4,
∵∠P= ![]() ∠AMB=∠AMN,
∠AMB=∠AMN,
∴tan∠APB=tan∠AMN= ![]() =
= ![]() .
.
故选B.
【考点精析】本题主要考查了切线的性质定理和解直角三角形的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.

(1)当OC∥AB时,∠BOC的度数为;
(2)连接AC,BC,当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC的面积的最大值;
(3)连接AD,当OC∥AD时,①求出点C的坐标;②直线BC是否为⊙O的切线?请作出判断,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】探究与应用.试完成下列问题:
(1)如图①,已知等腰Rt△ABC中,∠C=90°,点O为AB的中点,作∠POQ=90°,分别交AC、BC于点P、Q,连结PQ、CO,求证:AP2+BQ2=PQ2;
(2)如图②,将等腰Rt△ABC改为任意直角三角形,点O仍为AB的中点,∠POQ=90°,试探索上述结论AP2+BQ2=PQ2是否仍成立;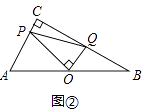
(3)通过上述探究(可直接运用上述结论),试解决下面的问题:如图③,已知Rt△ABC中,∠C=90°,AC=6,BC=8,点O为AB的中点,过C、O两点的圆分别交AC、BC于P、Q,连结PQ,求△PCQ面积的最大值.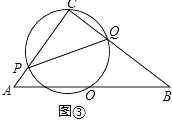
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图像记作抛物线E,现有点A(2,0)和抛物线E上的点B(﹣1,n),请完成下列任务;
(1)【尝试】①当t=2时,抛物线y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)的顶点坐标为
(2)②判断点A是否在抛物线E上;
(3)③求n的值.
(4)【发现】通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线E总过定点,坐标为 .
(5)【应用】
①二次函数y=﹣3x2+5x+2是二次函数y=x2﹣3x+3和一次函数y=﹣2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由;
②以AB为边作矩形ABCD,使得其中一个顶点落在y轴上;若抛物线E经过A,B,C,D其中的三点,求出所有符合条件的t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数与反比例函数的图像交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图像于点M、N,则四边形PMON面积的最大值是 .
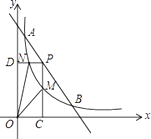
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|1﹣2sin45°|﹣
 +(
+(  )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】盐城市“创建文明城市”活动如火如荼的展开.某中学为了搞好“创建文明城市”活动的宣传,校学生会就本校学生对盐城“市情市况”的了解程度进行了一次调查测试.经过对测试成绩的分析,得到如下图所示的两幅不完整的统计图(A:59分及以下;B:60﹣69分;C:70﹣79分;D:80﹣89分;E:90﹣100分).请你根据图中提供的信息解答以下问题:

(1)求该校共有多少名学生;
(2)将条形统计图补充完整;
(3)在扇形统计图中,计算出“60﹣69分”部分所对应的圆心角的度数.
相关试题

