【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.

(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC,求∠CDO的大小.
参考答案:
【答案】(1)∠T==40°,∠CDB=40°;(2)∠CDO=15°.
【解析】试题分析:(1)根据切线的性质:圆的切线垂直于经过切点的半径,得∠TAB=90°,根据三角形内角和得∠T的度数,由直径所对的圆周角是直角和同弧所对的圆周角相等得∠CDB的度数;
(2)如图②,连接AD,根据等边对等角得:∠BCE=∠BEC=65°,利用同圆的半径相等知:OA=OD,同理∠ODA=∠OAD=65°,由此可得结论.
试题解析:(1)如图,连接AC,
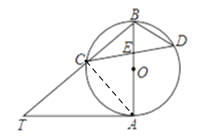
∵AB是⊙O的直径,AD是⊙O的切线,
∴AT⊥AB,即∠TAB=90°
∵∠ABT=50°,
∴∠T=90°-∠ABT=40°
由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90°-∠ABC=40°
∴∠CDB=∠CAB=40°;
(2)如图,连接AD
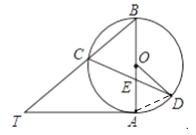
在△BCE中,BE=BC,∠EBC=50°,
∴∠BCE=∠BEC=65°,
∴∠BAD=∠BCD=65°
∵OA=OD
∴∠ODA=∠OAD=65°
∵∠ADC=∠ABC=50°
∴∠CDO=∠ODA-∠ADC=15°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
 绕点
绕点 顺时针旋转得到
顺时针旋转得到 ,使点
,使点 的对应点
的对应点 恰好落在边
恰好落在边 上,点
上,点 的对应点为
的对应点为 ,连接
,连接 .下列结论一定正确的是( )
.下列结论一定正确的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣3)﹣(﹣2)+(﹣4);
(2)﹣10+14+16﹣8;
(3)(-4)×(-5)-90÷(-15);
(4)﹣23÷
 ×(﹣
×(﹣ )2;
)2;(5)(
 +
+ ﹣
﹣ )×(﹣36);
)×(﹣36);(6)﹣14﹣
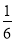 ×[2﹣(﹣3)2]
×[2﹣(﹣3)2] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E、F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=1,则四边形BEDF的周长是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在ABCD内部,AF∥BE,DF∥CE,设ABCD的面积为S1,四边形AEDF的面积为S2,则
 的值是_____.
的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB=|a﹣b|,回答下列问题:
(1)数轴上表示1和﹣3的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点分别是点A和B,如果AB=2,那么x= ;
(3)当|x﹣6|+|x﹣1|的最小值是 。若|x﹣3|+|x﹣b|的最小值为4,则b的值为 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线经过
 ,
,  ,
,  三点.
三点.(
 )求出抛物线的解析式.
)求出抛物线的解析式.(
 )
) 是抛物线上一动点,过
是抛物线上一动点,过 作
作 轴,垂足为
轴,垂足为 ,是否存在
,是否存在 点,使得以
点,使得以 ,
,  ,
, 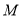 为顶点的三角形与
为顶点的三角形与 相似?若存在,请求出符合条件的点
相似?若存在,请求出符合条件的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

