搜索
【题目】已知△ABC是等边三角形，四边形ADEF是菱形，∠ADE=120°（AD＞AB）．
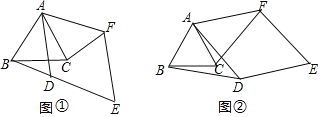
（1）如图①，当AD与边BC相交，点D与点F在直线AC的两侧时，BD与CF的数量关系为___________．
（2）将图①中的菱形ADEF绕点A在平面内逆时针旋转α（0°＜α＜180°）．
Ⅰ．判断（1）中的结论是否仍然成立，请利用图②证明你的结论．
Ⅱ．若AC=4，AD=6，当△ACE为直角三角形时，直接写出CE的长度．
【答案】（1）
；（2）I（1）中的结论仍然成立，理由详见解析；II
或
【解析】
（1）根据等式的性质得出∠BAD=∠CAF，利用SAS证明△ABD与△ACF全等，再利用全等三角形的性质得出即可；
（2）I．根据等式的性质得出∠BAD=∠CAF，利用SAS证明△ABD与△ACF全等，再利用全等三角形的性质得出即可；
II．当△ACE是直角三角形时，存在两种情况：
①如图2，当∠ACE=90°时，②如图3，当∠EAC=90°时，勾股定理即可得CE的长．
（1）解：如图①，∵四边形ADEF是菱形，∠ADE=120°，
∴AD=AF，∠DAF=60°，
∴∠DAC+∠CAF=60°，
∵△ABC是等边三角形，
∴AB=AC，∠BAC=60°，
∴∠BAD+∠DAC=60°，
∴∠BAD=∠CAF，
∴△BAD≌△CAF（SAS），
∴BD=CF；
故答案为：BD=CF；
（2）I．（1）中的结论仍然成立．
证明：如图②，∵△ABC是等边三角形，
∴AB=AC，∠BAC=60°，
在菱形ADEF中，
∴AD=AF，AF∥DE，
∴∠DAF=180°-∠ADE=180°-120°=60°，
∴∠BAC=∠DAF，
即∠BAC+∠CAD=∠DAF+∠CAD，
∴∠BAD=∠CAF，
∴△BAD≌△CAF，
∴BD=CF；
II．当△ACE是直角三角形时，存在两种情况：
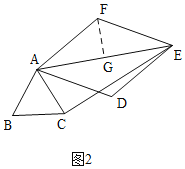
①如图2，当∠ACE=90°时，过F作FG⊥AE于G，
∵四边形ADEF是菱形，
∴AF=FE，∠AFE=∠ADE=120°，
∴∠AFG=60°，
∴∠FAG=30°，
∵AF=AD=6，
∴FG=3，
∴AG=3
，
∴AE=2AG=6，
Rt△ACE中，CE=
=；
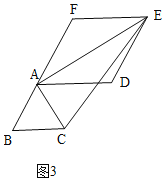
②如图3，当∠EAC=90°时，同理得：AE=6，
由勾股定理得：CE=
=
．
综上所述，CE的长为或．
