【题目】已知:正方形ABCD,E为平面内任意一点,连接DE,将线段DE绕点D顺时针旋转90°得到DG,连接EC,AG.
(1)当点E在正方形ABCD内部时, ①根依题意,在图1中补全图形;
②判断AG与CE的数量关系与位置关系并写出证明思路.
(2)当点B,D,G在一条直线时,若AD=4,DG=2 ![]() ,求CE的长.(可在备用图中画图)
,求CE的长.(可在备用图中画图) 
参考答案:
【答案】
(1)解:当点E在正方形ABCD内部时,
①根依题意,补全图形如图1:
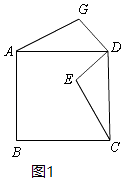
②AG=CE,AG⊥CE.
理由:
在正方形ABCD,
∴AD=CD,∠ADC=90°,
∵由DE绕着点D顺时针旋转90°得DG,
∴∠GDE=∠ADC=90°,GD=DE,
∴∠GDA=∠EDC
在△AGD和△CED中, 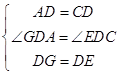 ,
,
∴△AGD≌△CED,
∴AG=CE.
延长CE分别交AG、AD于点F、H,
由①中结论△AGD≌△CED,
∴∠GAD=∠ECD,
∵∠AHF=∠CHD,
∴∠AFH=∠HDC=90°,
∴AG⊥CE.
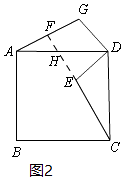
(2)解:①当点G在线段BD的延长线上时,如图3所示.
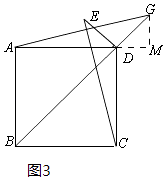
过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADB=∠GDM=45°.
∵GM⊥AD,DG=2 ![]()
∴MD=MG=2,
∴AM=AD+DM=6
在Rt△AMG中,由勾股定理,得
AG= ![]() =2
=2 ![]() ,
,
∴CE=AG=2 ![]()
②当点G在线段BD上时,如图4所示,
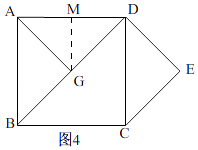
过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADG=45°
∵GM⊥AD,DG=2 ![]()
∴MD=MG=2,
∴AM=AD﹣MG=2
在Rt△AMG中,由勾股定理,得
AG= ![]() =2
=2 ![]()
∴CE=AG=2 ![]()
故CE的长为2 ![]() 或2
或2 ![]() .
.
【解析】(1)①根据题意补全图形,
②先判断出∠GDA=∠EDC,进而得出△AGD≌△CED,即可得出AG=CE,最后判断出∠AFH=∠HDC=90°即可得出结论;(2)分两种情况,①当点G在线段BD的延长线上时和②当点G在线段BD上时,构造直角三角形利用勾股定理即可得出结论.
【考点精析】解答此题的关键在于理解图形的旋转的相关知识,掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各运算中,计算正确的是( )
A.(x﹣2)2=x2﹣4
B.(3a2)3=9a6
C.x6÷x2=x3
D.x3x2=x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】设a﹣3b=5,则2(a﹣3b)2+3b﹣a﹣15的值是
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填表:
a
0.000 001
0.001
1
1 000
1 000 000
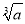
(2)由上表你发现了什么规律?请用语言叙述这个规律:_______________________;
(3)根据你发现的规律填空:
①已知
 =1.442,则
=1.442,则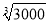 =________,
=________, 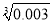 =__________;
=__________;②已知
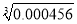 =0.076 97,则
=0.076 97,则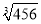 =__________.
=__________. -
科目: 来源: 题型:
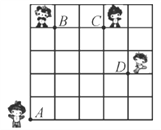
查看答案和解析>>【题目】如图,奥运福娃在5×5的方格(每小格边长为1 m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其他福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A·B(+1,+4),从B到A记为:B·A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中:
(1)A·C(__________,__________),B·C(__________,__________),C·__________(-3,-4);
(2)若贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出妮妮的位置点E.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业决定投资不超过20万元建造A、B两种类型的温室大棚.经测算,投资A种类型的大棚6万元/个、B种类型的大棚7万元/个,那么建造方案有( )
A.2种
B.3种
C.4种
D.5种 -
科目: 来源: 题型:
查看答案和解析>>【题目】如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表数据,从中选择一名成绩好且发挥稳定的参加比赛,应该选择( )
A. 甲 B. 乙 C. 丙 D. 丁
相关试题

