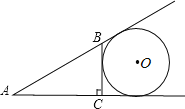
【题目】如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,求⊙O的半径.
参考答案:
【答案】2
【解析】试题分析:分析:先连接OD、OE根据⊙O与△ABC中AB、AC的延长线及BC边相切,得出AF=AD,BE=BF,CE=CD,再根据OD⊥AD,OE⊥BC,∠ACB=90°,得出四边形ODCE是正方形,最后设OD=r,列出5+3-r=4+r,求出r=2即可.
试题解析:
连接OD、OE,
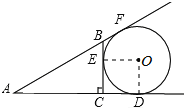
∵⊙O与△ABC中AB、AC的延长线及BC边相切,
∴AF=AD,BE=BF,CE=CD,
OD⊥AD,OE⊥BC,
∵∠ACB=90°,
∴四边形ODCE是正方形,
设OD=r,则CD=CE=r,
∵BC=3,
∴BE=BF=3-r,
∵AB=5,AC=4,
∴AF=AB+BF=5+3-r,
AD=AC+CD=4+r,
∴5+3-r=4+r,
r=2,
则⊙O的半径是2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为 ______
DM=BD+BE=4cm+4cm=8cm,
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,一条生产线的流水线上依次有5个机器人,它们站立的位置在数轴上依次用点A1,A2,A3,A4,A5表示.
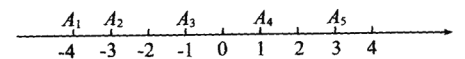
(1)若原点是零件的供应点,5个机器人分别到供应点取货的总路程是多少?
(2)若将零件的供应点改在A1,A3,A5中的其中一处,并使得5个机器人分别到达供应点取货的总路程最短,你认为应该在哪个点上?通过计算说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作
 ,与AC、DC分别交于点
,与AC、DC分别交于点 为CG的中点,连结DE、EH、DH、
为CG的中点,连结DE、EH、DH、 下列结论:
下列结论:  ;
;  ≌
≌ ;
;  ;
;  若
若 ,则
,则 其中结论正确的有
其中结论正确的有

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正五边形ABCDE中,对角线
 与EB分别相交于点
与EB分别相交于点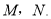 下列结论错误的是
下列结论错误的是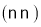
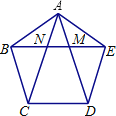
A. 四边形EDCN是菱形
B. 四边形MNCD是等腰梯形
C.
 与
与 相似
相似D.
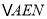 与
与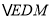 全等
全等 -
科目: 来源: 题型:
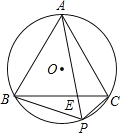
查看答案和解析>>【题目】如图,正
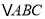 内接于
内接于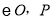 是劣弧BC上任意一点,PA与BC交于点E,有如下结论:
是劣弧BC上任意一点,PA与BC交于点E,有如下结论: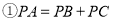 ;
; 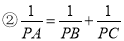 ;
; 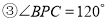 ;
;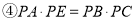 ;
; 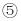 图中共有6对相似三角形.
图中共有6对相似三角形.其中,正确结论的个数为

A. 5个 B. 4个 C. 3个 D. 2个
相关试题

