【题目】如图,线段AB=10,动点P从点A出发,以每秒1个单位的速度,沿线段AB向终点B运动,同时,另一个动点Q从点B出发,以每秒3个单位的速度在线段AB上来回运动(从点B向点A运动,到达点A后,立即原速返回,再次到达B点后立即调头向点A运动.) 当点P到达B点时,P,Q两点都停止运动.设点P的运动时间为x. ![]()
(1)当x=3时,线段PQ的长为 .
(2)当P,Q两点第一次重合时,求线段BQ的长.
(3)是否存在某一时刻,使点Q恰好落在线段AP的中点上?若存在,请求出所有满足条件的x的值;若不存在,请说明理由.
参考答案:
【答案】
(1)2
(2)解:设x秒后P,Q第一次重合,得:x+3x=10
解得:x=2.5,
∴BQ=3x=7.5
(3)解:设x秒后,点Q恰好落在线段AP的中点上,根据题意,
①当点Q从点B出发未到点A时,即0<x< ![]() 时,有
时,有
x=2(10﹣3x),
解得 ![]() ;
;
②当点Q到达点A后,从A到B时,即 ![]() <x<
<x< ![]() 时,有
时,有
x=2(3x﹣10),
解得 x=4;
③当点Q第一次返回到B后,从B到A时,即 ![]() <x<10时,有
<x<10时,有
x=2(30﹣3x),
解得 ![]() ;
;
综上所述:当x= ![]() 或x=4或x=
或x=4或x= ![]() 时,点Q恰好落在线段AP的中点上
时,点Q恰好落在线段AP的中点上
【解析】解:(1)根据题意,当x=3时,P、Q位置如下图所示:![]()
此时:AP=3,BQ=3×3=9,AQ=AB﹣BQ=10﹣9=1,
∴PQ=AP﹣AQ=2;
故答案为: 2.
(1)结合图形,表示出AP、AQ的长,可得PQ;(2)当P,Q两点第一次重合时,点P运动路程+点Q运动路程=AB的长,列方程可求得;(3)点Q落在线段AP的中点上有以下三种情况:①点Q从点B出发未到点A;②点Q到达点A后,从A到B;③点Q第一次返回到B后,从B到A,根据AP=2AQ列方程可得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算6x(3–2x)的结果,与下列哪一个式子相同( )
A. –12x2+18x B. –12x2+3 C. 16x D. 6x
-
科目: 来源: 题型:
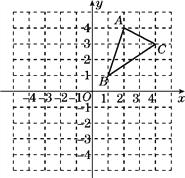
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).
-
科目: 来源: 题型:
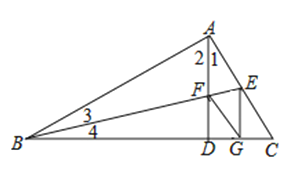
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD于F,交AC于E,若EG⊥BC于G,连结FG.说明四边形AFGE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把方程3x2﹣1=4x化为一般形式是: , 其一次项系数是 , 常数项是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=﹣2(x﹣1)2+3的图象的顶点坐标是 , 对称轴为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程(m﹣2)x2+5x+m2﹣2m=0的常数项为0,则m= .
相关试题

