【题目】如图，抛物线经过点、.是线段上一动点（点不与、重合），过点作轴的垂线交抛物线于点，交线段于点.过点作，垂足为点.

[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/18/2206393160556544/2207286529548288/STEM/a9696d0cbdac438aa94c80bfc838afd4.png]

（1）求该抛物线的解析式；

（2）试求线段的长关于点的横坐标的函数解析式，并求出的最大值.

【答案】（1）；（2）=，当时，取最大值，.

【解析】

（1）把代入解析式即可求出抛物线的解析式；（2）利用得，求得，再求出直线BC的解析式为，得点坐标为，坐标为

∴= ，即可表示出DF的函数为- ，即可求出最值.

（1）∵抛物线过点。

∴可得，解得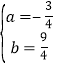

∴抛物线的解析式为

（2）∵

∴，∴

∴，∴

∴

∵，∴

∴

∵直线经过点

∴，∴点坐标为

∵点坐标为

∴

=

∴

=

=

∴当时，取最大值，

关闭