【题目】在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0,![]() ).
).
(1)求圆心C的坐标.
(2)抛物线y=ax2+bx+c过O,A两点,且顶点在正比例函数y=-![]() 的图象上,求抛物线的解析式.
的图象上,求抛物线的解析式.
(3)过圆心C作平行于x轴的直线DE,交⊙C于D,E两点,试判断D,E两点是否在(2)中的抛物线上.
(4)若(2)中的抛物线上存在点P(x0,y0),满足∠APB为钝角,求x0的取值范围.

参考答案:
【答案】(1)圆心C的坐标为(1,![]() );
);
(2)抛物线的解析式为y=![]() x2﹣
x2﹣![]() x;
x;
(3)点D、E均在抛物线上;
(4)﹣1<x0<0,或2<x0<3.
【解析】
试题分析:(1)如图线段AB是圆C的直径,因为点A、B的坐标已知,根据平行线的性质即可求得点C的坐标;
(2)因为抛物线过点A、O,所以可求得对称轴,即可求得与直线y=﹣![]() x的交点,即是二次函数的顶点坐标,利用顶点式或者一般式,采用待定系数法即可求得抛物线的解析式;
x的交点,即是二次函数的顶点坐标,利用顶点式或者一般式,采用待定系数法即可求得抛物线的解析式;
(3)因为DE∥x轴,且过点C,所以可得D、E的纵坐标为![]() ,求得直径AB的长,可得D、E的横坐标,代入解析式即可判断;
,求得直径AB的长,可得D、E的横坐标,代入解析式即可判断;
(4)因为AB为直径,所以当抛物线上的点P在⊙C的内部时,满足∠APB为钝角,所以﹣1<x0<0,或2<x0<3.
试题分析:(1)∵⊙C经过原点O
∴AB为⊙C的直径
∴C为AB的中点
过点C作CH垂直x轴于点H,则有CH=![]() OB=
OB=![]() ,OH=
,OH=![]() OA=1
OA=1
∴圆心C的坐标为(1,![]() ).
).
(2)∵抛物线过O、A两点,
∴抛物线的对称轴为x=1,
∵抛物线的顶点在直线y=﹣![]() x上,
x上,
∴顶点坐标为(1,﹣![]() ).
).
把这三点的坐标代入抛物线y=ax2+bx+c,得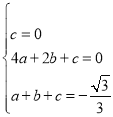 ,
,
解得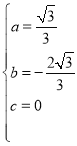 ,
,
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x.
x.
(3)∵OA=2,OB=2![]() ,
,
∴AB=![]() =4,即⊙C的半径r=2,
=4,即⊙C的半径r=2,
∴D(3,![]() ),E(﹣1,
),E(﹣1,![]() ),
),
代入y=![]() x2﹣
x2﹣![]() x检验,知点D、E均在抛物线上.
x检验,知点D、E均在抛物线上.
(4)∵AB为直径,
∴当抛物线上的点P在⊙C的内部时,满足∠APB为钝角,
∴﹣1<x0<0,或2<x0<3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:ab2﹣9a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形两边长分别为3和8,第三边长为奇数,则第三边长为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】-32的值是( )
A.-9
B.9
C.-6
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】台湾是我国最大的岛屿,总面积为35989.76平方千米,这个数字用科学计数法表示为_____平方千米(精确到百位).
-
科目: 来源: 题型:
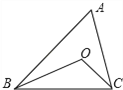
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=80°,则∠BOC=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=A1B,在AA1的延长线上依次取A2、A3、A4、…、An,并依次在三角形的外部作等腰三角形,使A1C1=A1A2,A2C2=A2A3,A3C3=A3A4,…,An﹣1Cn﹣1=An﹣1An.
记∠BA1A=∠1,∠C1A2A1=∠2,……,以此类推. 若∠B=30°,则∠n=_________°.

相关试题

