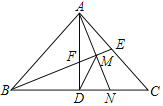
【题目】如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM,下列结论:①AE=AF;②DF=DN;③AN=BF;④EN⊥NC;⑤AE=NC,其中正确结论的个数是( )
A. 2个B. 3个C. 4个D. 5个
参考答案:
【答案】D
【解析】
①根据等腰直角三角形的性质及角平分线的定义求得![]() ,继而可得∠AFE=∠AEB=67.5°,即可判断①;
,继而可得∠AFE=∠AEB=67.5°,即可判断①;
②求出BD=AD,∠DBF=∠DAN,∠BDF=∠ADN,证△DFB≌△DAN,即可判断②;
③根据A、B、D、M四点共圆求出∠ADM=22.5°,根据三角形外角性质求出∠DNM,求出∠MDN=∠DNM,即可判断③;
④求出∠BMD=45°=∠BMN,即可判断④;
⑤证明△AFB≌△CNA可得AF=CN,由AF=AE,即可判断⑤.
解:∵等腰Rt△ABC中,∠BAC=90°,AD⊥BC,
∴∠BAD=∠CAD=∠C=45°,
∵∵BE平分∠ABC,
∴∠ABE=∠CBE=![]() ∠ABC=22.5°,
∠ABC=22.5°,
∴∠AEF=∠CBE+∠C=22.5°+45°=67.5°,∠AFE=∠FBA+∠BAF=22.5°+45°=67.5°
∴∠AEF=∠AFE,
∴AE=AF,
故①正确;
∵∠BAC=90°,AC=AB,AD⊥BC,
∴∠ABC=∠C=45°,AD=BD=CD,∠ADN=∠ADB=90°,
∴∠BAD=45°=∠CAD,
∵BE平分∠ABC,
∴∠ABE=∠CBE=![]() ∠ABC=22.5°,
∠ABC=22.5°,
∴∠BFD=∠AEB=90°﹣22.5°=67.5°,
∴AFE=∠BFD=∠AEB=67.5°,
∴AF=AE,AM⊥BE,
∴∠AMF=∠AME=90°,
∴∠DAN=90°﹣67.5°=22.5°=∠MBN,
在△FBD和△NAD中
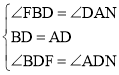 ,
,
∴△FBD≌△NAD(ASA),
∴DF=DN,AN=BF,
∴②③正确;
连接EN,
∵AE=AF,FM=EM,
∴AM⊥EF,
∴∠BMA=∠BMN=90°,
∵BM=BM,∠MBA=∠MBN,
∴△MBA≌△MBN,
∴AM=MN,
∴BE垂直平分线段AN,
∴AB=BN,EA=EN,
∵BE=BE,
∴△ABE≌△NBE,
∴∠ENB=∠EAB=90°,
∴EN⊥NC.
故④正确;
在△AFB和△CNA中,
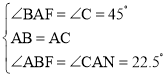 ,
,
∴△AFB≌△CAN(ASA),
∴AF=CN,
∵AF=AE,
∴AE=CN,
故⑤正确;
其中正确结论的个数是:①②③④⑤,共5个;
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】把正方体的六个面分别涂上六种不同的颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
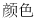
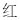



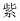
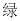
现将上述大小相同,颜色、花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问:长方体的下底面共有多少朵花?
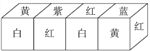
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A城气象台测得台风中心在A城正西方向320 km的B处,以每小时40 km的速度向北偏东60°的BF方向移动,距离台风中心200 km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点和⊙O,给出如下定义:过点A的直线l交⊙O于B,C两点,且A、B、C三点不重合,若在A、B、C三点中,存在位于中间的点恰为以另外两点为端点线段的中点时,则称点A为⊙O的价值点.
(1)如图1,当⊙O的半径为1时.
①分别判断在点D(
 ,
, ),E(﹣1,
),E(﹣1, ),F(2,3)中,是⊙O的价值点有 ;
),F(2,3)中,是⊙O的价值点有 ;②若点P是⊙O的价值点,点P的坐标为(x,0),且x>0,则x的最大值为 .
(2)如图2,直线y=﹣
 x+3与x轴,y轴分别交于M、N两点,⊙O半径为1,直线MN上是否存在⊙O的价值点?若存在,求出这些点的横坐标的取值范围,若不存在,请说明理由;
x+3与x轴,y轴分别交于M、N两点,⊙O半径为1,直线MN上是否存在⊙O的价值点?若存在,求出这些点的横坐标的取值范围,若不存在,请说明理由;(3)如图3,直线y=﹣
 x+2
x+2 与x轴、y轴分别交于G、H两点,⊙C的半径为1,且⊙C在x轴上滑动,若线段GH上存在⊙C的价值点P,求出圆心C的横坐标的取值范围.
与x轴、y轴分别交于G、H两点,⊙C的半径为1,且⊙C在x轴上滑动,若线段GH上存在⊙C的价值点P,求出圆心C的横坐标的取值范围.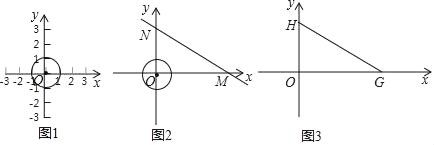
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90o,AB=AD,AE=AC, AF⊥CF,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:AC平分∠ECF;
(3)求证:CE=2AF .

相关试题

