【题目】如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24 m,OE⊥CD于点E.已测得sin∠DOE=![]() .
.
(1)求半径OD;
(2)根据需要,水面要以每小时0.5m的速度下降,则经过多长时间才能将水排干?

参考答案:
【答案】解:(1) ∵0E⊥CD于点E,CD=24,
∴ED=![]() CD=12. ……2分
CD=12. ……2分
在Rt△DOE中,∵sin DOE=![]() =
=![]() ,
,
∴OD=13m. ……6分
(2) OE=![]() ……8分
……8分
=![]() =5. ……10分
=5. ……10分
∴将水排干需:5÷0.5=10(h). ……12分
【解析】试题分析:根据三角函数可得到OD的值;再根据勾股定理求得OE的值,此时再求所需的时间就变得容易了.
试题解析:(1)∵OE⊥CD于点E,CD=24,
∴ED=![]() CD=12,
CD=12,
在Rt△DOE中,
∵sin∠DOE=![]() ,
,
∴OD=13(m);
(2)OE=![]() =5,
=5,
∴将水排干需:5÷0.5=10(小时).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.
求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】如果P(a+b,ab)在第二象限,那么点Q(a,﹣b)在第象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=
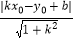 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=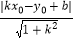 =
= 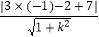 =
= 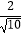 =
= 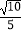 .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=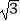 x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( )

A.2
B.4
C.4
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACE是以ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,﹣3
 ),则D点的坐标是 .
),则D点的坐标是 . 
相关试题

