【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP,并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连接AP,并延长交BC于点D,则下列说法中正确的个数是( )

①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④若AC=![]() dm,AD=2dm,则点D到AB的距离是1dm;⑤S△DAC∶S△DAB=AC∶AB=1∶2
dm,AD=2dm,则点D到AB的距离是1dm;⑤S△DAC∶S△DAB=AC∶AB=1∶2
A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】D
【解析】①根据作图的过程可知,AD是∠BAC的平分线;故①正确;
②如图,
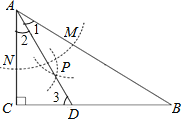
∵在△ABC中,∠C=90,∠B=30°,∴∠CAB=60°.
又∵AD是∠BAC的平分线,∴∠1=∠2=![]() ∠CAB=30°,
∠CAB=30°,
∴∠3=90°∠2=60°,即∠ADC=60°.故②正确;
③∵∠1=∠B=30°,∴AD=BD,∴点D在AB的垂直平分线上;故③正确;
④∵∠C=90°,AC=![]() dm,AD=2dm,∴CD=1cm,
dm,AD=2dm,∴CD=1cm,
如图,过D作DE⊥AB于点E,
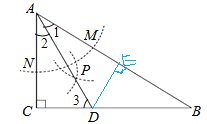
∵AD是∠CAB的平分线,DC⊥AC,DE⊥AB,
∴CD=ED, ∴ED=1cm,故④正确;
(5)在直角△ACD中,∠2=30°,
∴CD=![]() AD,
AD,
∴BC=CD+BD=![]() AD+AD=
AD+AD=![]() AD,S△DAC=
AD,S△DAC=![]() ACCD=
ACCD=![]() ACAD.
ACAD.
∴S△ABD=![]() ACBD=
ACBD=![]() ACAD=
ACAD=![]() ACAD,
ACAD,
∴S△DAC:S△ABD=![]() ACAD:
ACAD: ![]() ACAD=1:2.故⑤正确.
ACAD=1:2.故⑤正确.
综上所述,正确的结论是:①②③④⑤.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=b,则下列等式不成立的是( )
A.a+1=b+1B.1﹣a=1﹣bC.3a=3bD.2﹣3a=3b﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;②∠DFB=
 ∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的个数是( )
∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
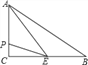
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=_____________,△APE的面积等于6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如右图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.

(1)请在图中画出平移后的△ABC
(2)再在图中画出△ABC的高CD
(3)
 =
= (4)在右图中能使
 的格点P的个数有 个(点P异于A) .
的格点P的个数有 个(点P异于A) . -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项式乘方(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)64的展开式中第三项的系数为( )
A. 2016 B. 2017 C. 2018 D. 2019
相关试题

