[题目]在平面直角坐标系xOy中.直线与双曲线()的一个交点为．(1)求k的值,(2)将直线向上平移b(b>0)个单位长度后.与x轴.y轴分别交于点A.点B.与双曲线()的一个交点记为Q．若.求b的值．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】在平面直角坐标系xOy中，直线与双曲线（）的一个交点为．

（1）求k的值；

（2）将直线向上平移b(b>0)个单位长度后，与x轴，y轴分别交于点A，点B，与双曲线（）的一个交点记为Q．若，求b的值．

【答案】（1）（2）或

【解析】

（1）根据已知条件可知，把的横纵坐标代入即可确定点，再将其代入即可求得答案；

（2）由平移可知，，再对点的位置进行分类讨论，分别画出相应的图形构造出相似三角形即可得到关于的方程，解方程即可得解．

解：（1）∵在直线上

∴当时，

∴

∵在双曲上

∴；

（2）∵将直线向上平移个单位长度后，与轴，轴分别交于点，点

∴，

①当点在第二象限时，过作轴于点，如图：

∴

∵

∴

∵，

∴，

∵点在第二象限，

∴

∵在双曲上

∴

∵

∴；

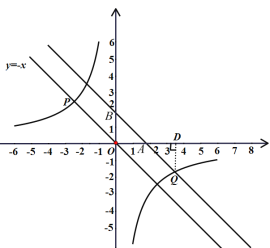
②当点在第四象限时，过作轴于点，如图：

∴

∵

∴

∵，

∴，

∵点在第四象限，

∴

∵在双曲上

∴

∵

∴．

∴综上所述，或．

故答案是：（1）（2）或

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图抛物线的开口向下与轴交于点和点，与轴交于点，点是抛物线上一个动点(不与点重合)

(1)求抛物线的解析式；

(2)当点是抛物线上一个动点，若的面积为12，求点的坐标；

(3)如图2，抛物线的顶点为，在抛物线上是否存在点，使得，若存在请直接写出点的坐标；若不存在请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，点是所对弦上一动点，点在的延长线上，过点作交于点，连接，已知，，设，两点间的距离为，的面积为．（当点与点，重合时，的值为0．）

小亮根据学习函数的经验，对函数随自变量的变化而变化的规律进行了探究．

下面是小亮的探究过程，请补充完整：

（1）通过取点、画图、测量，得到了与的几组值，如下表：

	3	4	5	6	7	8	9
	0	4.47	7.07	9.00		8.94	0

（2）在平面直角坐标系中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；

（3）结合画出的函数图象，解决问题：当的面积为时，的长度约为　　．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】数学活动课上，老师提出问题：如图1，在Rt△ABC中，∠C＝90°，BC＝4cm，AC＝3cm，点D是AB的中点，点E是BC上一个动点，连接AE、DE．问CE的长是多少时，△AED的周长等于CE长的3倍．设CE＝xcm，△AED的周长为ycm（当点E与点B重合时，y的值为10）．

小牧根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．

下面是小牧的探究过程，请补充完整：

（1）通过取点、画图、测量，得到了x与y的几组值，如下表：

x/cm	0	0.5	1	1.5	2	2.5	3	3.5	4
y/cm	8.0	7.7	7.5	7.4		8.0	8.6	9.2	10

（说明：补全表格时相关数值保留一位小数）

（2）建立平面直角坐标系，描出上表中对应值为坐标的点，画出该函数的图象，如图2；

（3）结合画出的函数图象，解决问题：

①当CE的长约为　　cm时，△AED的周长最小；

②当CE的长约为　　cm时，△AED的周长等于CE的长的3倍．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】对于平面直角坐标系xOy中的点P和⊙C，给出如下定义：若存在过点P的直线l交⊙C于异于点P的A，B两点，在P，A，B三点中，位于中间的点恰为以另外两点为端点的线段的中点时，则称点P为⊙C 的相邻点，直线l为⊙C关于点P的相邻线．

（1）当⊙O的半径为1时，

①分别判断在点D（，），E（0，），F（4，0）中，是⊙O的相邻点有__________；

②请从①中的答案中，任选一个相邻点，在图1中做出⊙O关于它的一条相邻线，并说明你的作图过程．

③点P在直线上，若点P为⊙O的相邻点，求点P横坐标的取值范围；

（2）⊙C的圆心在x轴上，半径为1，直线与x轴，y轴分别交于点M，N，若线段MN上存在⊙C的相邻点P，直接写出圆心C的横坐标的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（1）在浙江卫视全新推出的大型户外竞技真人秀节目﹣﹣《奔跑吧兄弟》中，七位主持人邓超、王祖蓝、王宝强、李晨、陈赫、郑凯及Angelababy（杨颖）在“撕名牌环节”的成绩分别为：8，5，7，8，6，8，5，则这组数据的众数和中位数分别是　　．

（2）某学校想了解学生对撕名牌游戏的喜欢程度，对学校部分学生进行了抽样调查，就学生对游戏的喜欢程度（A：喜欢；B：一般；C：不喜欢；D：无所谓）进行数据统计，并绘制了如下两幅不完整的统计图．

①此次调查的样本容量为　　；

②条形统计图中存在的错误是　　（填A、B、C中的一个）；

③在图2中补画条形统计图中不完整的部分；

④若从该校喜欢撕名牌游戏的学生中抽取10人进行比赛，则喜欢撕名牌游戏的小明被抽中的概率是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，抛物线与轴相交于点、，与轴相交于点，过点作，与抛物线相交于点．点从点出发，在折线段上以每秒2个单位长度向終点勾速运动，点从点出发，在线段上以每秒1个单位长度向终点匀速运动，两点同时出发，当其中一个点到达终点时，另一个点也停止运动，连接．设点的运动时间为，线段的长度的平方为，即（单位长度），