【题目】一艘渔船从港口A沿北偏东60°方向航行至C处时突然发生故障,在C处等待救援.有一救援艇位于港口A正东方向20(![]() ﹣1)海里的B处,接到求救信号后,立即沿北偏东45°方向以30海里/小时的速度前往C处救援.则救援艇到达C处所用的时间为( )
﹣1)海里的B处,接到求救信号后,立即沿北偏东45°方向以30海里/小时的速度前往C处救援.则救援艇到达C处所用的时间为( )

A. ![]() 小时 B.
小时 B. ![]() 小时 C.
小时 C. ![]() 小时 D.
小时 D. ![]() 小时
小时
参考答案:
【答案】C
【解析】
过点C作CD垂直AB延长线于D,根据题意得∠CDB=45°,∠CAD=30°,设BD=x则CD=BD=x,BC=![]() x,由∠CAD=30°可知tan∠CAD=
x,由∠CAD=30°可知tan∠CAD=![]() 即
即![]() ,解方程求出BD的长,从而可知BC的长,进而求出救援艇到达C处所用的时间即可.
,解方程求出BD的长,从而可知BC的长,进而求出救援艇到达C处所用的时间即可.
如图:过点C作CD垂直AB延长线于D,则∠CDB=45°,∠CAD=30°,
∵∠CDB=45°,CD⊥BD,
∴BD=CD,
设BD=x,救援艇到达C处所用的时间为t,
∵tan∠CAD=![]() ,AD=AB+BD,
,AD=AB+BD,
∴![]() ,得x=20(海里),
,得x=20(海里),
∴BC=![]() BD=20
BD=20![]() (海里),
(海里),
∴t=![]() =
=![]() (小时),
(小时),

故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E是BC边的中点,连接DE并延长交AB的延长线于点F,则在题中条件下,下列结论不能成立的是( )
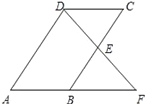
A. BE=CE B. AB=BF C. DE=BE D. AB=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格出售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(
 ,
,  )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.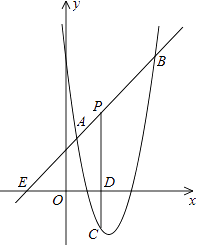
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形均是一些科技创新公司标志图,其中既是中心对称图形又是轴对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,F分别在边BC,CD上,且BE=CF.连接AE,BF,AE与BF交于点G.下列结论错误的是( )
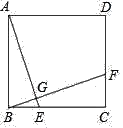
A. AE=BF B. ∠DAE=∠BFC
C. ∠AEB+∠BFC=90° D. AE⊥BF
相关试题

