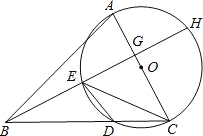
【题目】已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧![]() 上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接AD,由圆周角定理即可得出∠DAC=∠DEC,∠ADC=90°,再根据直角三角形的性质即可得出结论;
(2)由∠BDA=180°-∠ADC=90°,∠ABC=45°可求出∠BAD=45°,利用勾股定理即可得出DC的长,进而求出BC的长,由已知的一对角线段和公共角,根据两对对应角相等的两三角形相似可得三角形BCE与三角形EDC相似,由相似得比例即可求出CE的长.
试题解析:(1)连接AD,
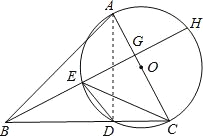
∵∠DAC=∠DEC,∠EBC=∠DEC,
∴∠DAC=∠EBC,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠DCA+∠DAC=90°,
∴∠EBC+∠DCA=90°,
∴∠BGC=180°-(∠EBC+∠DCA)=180°-90°=90°,
∴AC⊥BH;
(2)∵∠BDA=180°-∠ADC=90°,∠ABC=45°,
∴∠BAD=45°,
∴BD=AD,
∵BD=8,∴AD=8,
在直角三角形ADC中,AD=8,AC=10,
根据勾股定理得:DC=6,则BC=BD+DC=14,
∵∠EBC=∠DEC,∠BCE=∠ECD,
∴△BCE∽△ECD,
∴![]() ,即CE2=BCCD=14×6=84,
,即CE2=BCCD=14×6=84,
∴CE=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地市话的收费标准为:(1)通话时间在3分钟以内(包括3分钟)话费0.3元;(2)通话时间超过3分钟时,超过部分的话费按每分钟0.11元计算.在一次通话中,如果通话时间超过3分钟,那么话费y(元)与通话时间x(分)之间的关系式为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从多边形的一个顶点出发能画5条对角线,则这个多边形的边数是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当2x+1和﹣3x+2互为相反数时,则x2﹣2x+1=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生的课余生活,某中学在全校范围内随机抽取部分学生进行问卷调查,问卷中请学生选择最喜欢的课余生活种类(每人只选一类),选项有音乐类、美术类、体育类及其他共四类.调查后将数据绘制成扇形统计图和条形统计图(如图所示).
(1)请根据所给的扇形图和条形图,直接填写出扇形图中缺失的数据,并把条形图补充完整;
(2)在扇形统计图中,音乐类选项所在的扇形的圆心角的大小为 °;
(3)这所中学共有学生1200人,求喜欢音乐和美术类的课余生活共有多少人?
(4)在问卷调查中,小丁和小李分别选择了音乐类和美术类,校学生会要从选择音乐类和美术类的学生中分别抽取一名学生参加活动,用列表或画树状图的方法求小丁和小李恰好都被选中的概率.

-
科目: 来源: 题型:
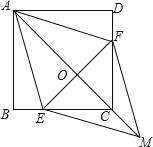
查看答案和解析>>【题目】如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:CE=CF.
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2﹣4b2= .
相关试题

