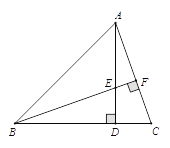
【题目】如图,AD是△ABC一边上的高,BF⊥AC,BE=AC.(1)求证:AD=BD;(2)若∠C=65°,求∠ABE的度数.
参考答案:
【答案】(1)证明见解析;(2)20°
【解析】试题分析:(1)利用同角的余角相等求出∠C=∠BED,再利用“角角边”证明△ACD和△BED全等,根据全等三角形对应边相等证明即可;
(2)根据直角三角形两锐角互余求出∠FBC,再求出△ABD是等腰直角三角形,根据等腰直角三角形的性质求出∠ABD=45°,再根据∠ABE=∠ABD-∠CBF代入数据计算即可得解.
试题解析:(1)证明:∵AD是△ABC一边上的高,BF⊥AC,
∴∠C+∠CBE=90°,
∠BED+∠CBE=90°,
∴∠C=∠BED,
在△ACD和△BED中,

∴△ACD≌△BED(AAS),
∴AD=BD;
(2)∵BF⊥AC,
∴∠CBF=90°-∠C=90°-65°=25°,
∵AD⊥BC,AD=BD,
∴△ABD是等腰直角三角形,
∴∠ABD=45°,
∴∠ABE=∠ABD-∠CBF=45°-25°=20°.
-
科目: 来源: 题型:
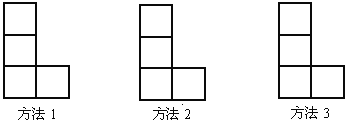
查看答案和解析>>【题目】① 如图,由小正方形组成的L形图中,用三种方法分别在图中添一个小正方形使图形成为轴对称图形:
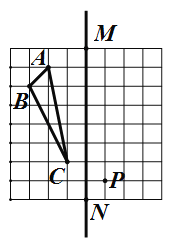
② 如图,在正方形网格上的一个△ABC.
⑴ 作△ABC关于直线MN的对称图形(不写作法);
⑵ 以P为一个顶点作与△ABC全等的三角形(规定点P与点B对应,另两顶点都在图中网格交点处),则可作出 个三角形与△ABC全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作探究:(1)现有一块等腰三角形纸板,量得周长为32cm,底比一腰多2cm.若把这个三角形纸板沿其对称轴剪开,拼成一个四边形,请画出你能拼成的各种四边形的示意图
(2)计算拼成的各个四边形的两条对角线长的平方和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个城镇A、B与两条公路l1、l2位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中,用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC=5,BC=6,以AC为一边作正方形ACDE,过点D作DF⊥BC交直线BC于点F,连接AF,请你画出图形,直接写出AF的长,并画出体现解法的辅助线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(Ⅰ)计算AC2+BC2的值等于 ;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使该矩形的面积等于AC2+BC2,并简要说明画图方法(不要求证明) .
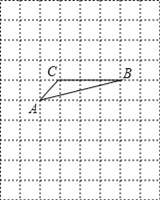
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件服装标价200元,若以6折销售,仍可获利20%,则这件服装的进价是( )
A. 100元 B. 105元 C. 108元 D. 118元
相关试题

