【题目】某公司欲招聘一名公务人员,对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如表所示:
应试者 | 面试 | 笔试 |
甲 | 86 | 90 |
乙 | 92 | 83 |
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为作为公务人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
参考答案:
【答案】(1)甲将被录取;(2)乙将被录取.
【解析】
(1)求得面试和笔试的平均成绩即可得到结论;
(2)根据题意先算出甲、乙两位应聘者的加权平均数,再进行比较,即可得出答案.
解:(1)![]() =
=![]() =89(分),
=89(分),
![]() =
=![]() =87.5(分),
=87.5(分),
因为![]() >
>![]() ,
,
所以认为面试和笔试成绩同等重要,从他们的成绩看,甲将被录取;
(2)甲的平均成绩为:(86×6+90×4)÷10=87.6(分),
乙的平均成绩为:(92×6+83×4)÷10=88.4(分),
因为乙的平均分数较高,
所以乙将被录取.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则sinB=
 ,sinC=
,sinC= ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 ,同理有:
,同理有: ,
, ,所以
,所以 .
.即:在一个三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来,我国政府灵活应对,现如今已对钓鱼岛执行常态化巡逻.某次巡逻中,如图(3),我渔政204船在C处测得A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政204船距钓鱼岛A的距离AB.(结果精确到0.01,
 ≈2.449)
≈2.449) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E为AD的延长线上一点,且DE=DC,点P为边AD上一动点,且PC⊥PG,PG=PC,点F为EG的中点.当点P从D点运动到A点时,则CF的最小值为___________
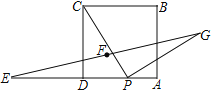
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条河的北岸有两个目标M、N,现在位于它的对岸设定两个观测点A、B.已知AB∥MN,在A点测得∠MAB=60°,在B点测得∠MBA=45°,AB=600米.
(1)求点M到AB的距离;(结果保留根号)
(2)在B点又测得∠NBA=53°,求MN的长.(结果精确到1米)
(参考数据:
 ≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)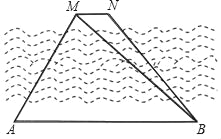
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆桌面(桌面中间有一个直径为1m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为2m,桌面离地面1m,若灯泡离地面2m,则地面圆环形阴影的面积是( )
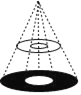
A. 2πm2 B. 3πm2 C. 6πm2 D. 12πm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆O的直径,C是半圆上一点,且∠BOC=60°,设弓形AmC,△AOC,扇形BOC的面积分别为S1,S2,S3,则它们之间的大小关系是( )
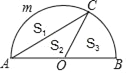
A. S1<S2<S3 B. S2<S1<S3 C. S2<S3<S1 D. S3<S2<S1
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l1∥l2∥l3,且l1与l2的距离为1.l2与l3的距离为2,把∠ACB=30°的直角三角板如图放置,顶点A,B,C恰好落在三条直线上,则线段AB的长为_____.

相关试题

