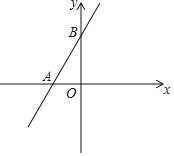
【题目】已知直线AB的函数表达式为y=![]() x+4,交x轴于点A,交y轴于点B,动点C从点A出发,以每秒2个单位长度的速度沿x轴正方向运动,设运动时间为t秒.
x+4,交x轴于点A,交y轴于点B,动点C从点A出发,以每秒2个单位长度的速度沿x轴正方向运动,设运动时间为t秒.
(1)求点A、B两点的坐标;
(2)当t为何值时,经过B、C两点的直线与直线AB关于y轴对称?并求出直线BC的函数关系式;
(3)在第(2)问的前提下,在直线AB上是否存在一点P,使得S△BCP=2S△ABC?如果存在,请求出此时点P的坐标;如果不存在,请说明理由.
参考答案:
【答案】(1)B(0,4),A(﹣3,0);(2)t=3秒,直线BC解析式为:y=﹣![]() x+4;(3)见解析.
x+4;(3)见解析.
【解析】
(1)令=0,则y=4可求出点B的坐标,令y=0,则0=![]() x+4可求得点A的坐标;
x+4可求得点A的坐标;
(2)先求出点A′的坐标,即点C的坐标,运用待定系数法可得直线BC的解析式;
(3)分两种情况:当点P在第三象限时,当点P在第一象限时分别求解即可.
(1)令=0,则y=4,
则点B(0,4),
令y=0,则0=![]() x+4,解得:x=﹣3,
x+4,解得:x=﹣3,
则点A(﹣3,0).
(2)点A关于y轴点对称点为A′(3,0),
所以当点C运动到A′(3,0)时,直线BC与直线AB关于y轴对称,则t=![]() =3秒.
=3秒.
设此时直线BC的解析式为:y=kx+b.
把点C(3,0)和点B(0,4)代入得:![]() ,
,
解得: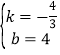 .
.
故直线BC解析式为:y=﹣![]() x+4.
x+4.
(3)存在,如图,当点P在第三象限时,S△BCP=2S△ABC,则S△ACP=S△ABC,
∴点P到x轴的距离等于点B到x轴的距离,
∴点P的纵坐标为﹣4,
把y=﹣4代入到y=![]() x+4中得:﹣4=
x+4中得:﹣4=![]() x+4,
x+4,
解得:x=﹣6,
则P(﹣6,﹣4);
当点P在第一象限时,S△BCP=2S△ABC,则S△ACP=3S△ABC,
∴点P到x轴的距离等于点B到x轴的距离,
∴点P的纵坐标为12,
把y=12代入到y=![]() x+4中得:12=
x+4中得:12=![]() x+4,
x+4,
解得:x=6,
则P'(6,12),
即:点P的坐标为(﹣6,﹣4)或(6,12).

-
科目: 来源: 题型:
查看答案和解析>>【题目】位于红星路济宁师专旧址的济宁学院附中红星校区将于近期开始动工,原计划在年内拆除旧校舍与建造新校舍共12万平方米,为建设一座园林式的校园,在实施中调整拆建计划,新建面积减少10%,拆除面积增加10%,结果拆除和新建总面积不变.根据协议,施工方免费拆除旧校舍,但建造新校舍每平米需要1500元,校园环境建设每平方米需要600元.
(1)求原计划拆、建的面积各多少平方米?
(2)若把实际的拆、建工程中节余的资金的30%用来增加校园环境建设,可建设多少平方米?
-
科目: 来源: 题型:
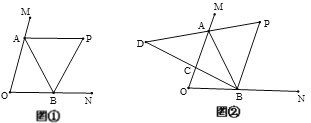
查看答案和解析>>【题目】如图①,∠MON=70°,点A、B在∠MON的两条边上运动,∠MAB与∠NBA的平分线交于点P.
(1)点A、B在运动过程中,∠P的大小会变吗?如果不会,求出∠P的度数;如果会,请说明理由.
(2)如图②,继续作BC是平分
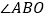 ,AP的反向延长线交BC的延长线于点D,点A、B在运动过程中,∠D的大小会变吗?如果不会,求出∠D的度数;如果会,请说明理由.
,AP的反向延长线交BC的延长线于点D,点A、B在运动过程中,∠D的大小会变吗?如果不会,求出∠D的度数;如果会,请说明理由.(3)如图②,∠P和∠D有怎样的数量关系?(直接写出答案)
-
科目: 来源: 题型:
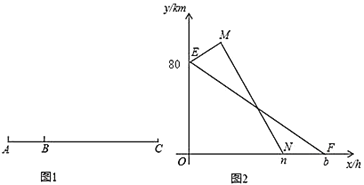
查看答案和解析>>【题目】如图有A、B、C三地依次在一条笔直的公路上,A、B两地相距40km,一辆甲车以40km/h的速度从B地到C地;同时一辆乙车以80km/h的速度从B地开往A地,到达A地后,然后以120km/h的速度开往C地,两车在各段内均匀速行驶,图中线段EF与折线EMN分别表示甲、乙两车距C地的路程y(千米)与行驶时间x(小时)之间的函数关系图象.
(1)写出点M的坐标为_______;点E的纵坐标的意义是________.
(2)请直接写出n,b的值,并求出线段EF与MN的函数关系式;
(3)两车出发几小时后,乙车追上甲车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
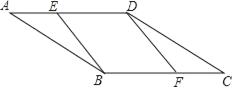
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
-
科目: 来源: 题型:
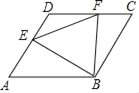
查看答案和解析>>【题目】如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a,△BEF的周长最小值是( )
A.
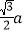 B.
B. 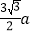 C.
C. 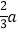 D.
D. 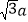
相关试题

