【题目】在平面直角坐标系中,A、B、C三点的坐标分别为![]() 、
、![]() 、
、![]() .
.
![]() 画出
画出![]() ,并求
,并求![]() 的面积;
的面积;
![]() 在
在![]() 中,点C经过平移后的对应点为
中,点C经过平移后的对应点为![]() ,将
,将![]() 作同样的平移得到
作同样的平移得到![]() ,画出平移后的
,画出平移后的![]() ,并写出点
,并写出点![]() ,
,![]() 的坐标;
的坐标;
![]() 已知点
已知点![]() 为
为![]() 内一点,将点P向右平移4个单位后,再向下平移6个单位得到点
内一点,将点P向右平移4个单位后,再向下平移6个单位得到点![]() ,则
,则![]() ______,
______,![]() ______.
______.
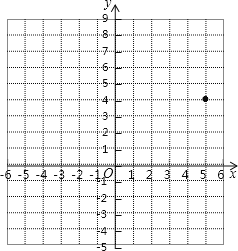
参考答案:
【答案】(1)图形见解析,S△ABC=15;(2)图形见解析,A′的坐标为(-1,8),点B′的坐标为(2,1);(3)3,1.
【解析】
(1)按题中要求描出A、B、C三点,并顺次连接三点即可得到△ABC如下图所示,再由S△ABC=S矩形ADOE-S△ABD-S△BOC-S△ACE结合图形即可求得△ABC的面积;
(2)由点C(0,3)平移后得到点C′(5,4)可知,把△ABC向右平移5个单位长度,再向上平移1个单位长度即可得到△A′B′C′,画出△A′B′C′并结合图形写出点A′和B′的坐标即可;
(3)根据“点的坐标变化与点的平移间的关系”结合已知条件进行分析解答即可.
(1)如下图,△ABC为所求三角形,结合已知条件和图形可得:
S△ABC=S矩形ADOE-S△ABD-S△BOC-S△ACE
=![]()
=![]()
=![]() .
.

(2)由点C(0,3)平移后得到点C′(5,4)可知,把△ABC向右平移5个单位长度,再向上平移1个单位长度即可得到△A′B′C′,
如上图所示,图中的△A′B′C′为所求三角形,其中点A′的坐标为(-1,8),点B′的坐标为(2,1);
(3)∵点![]() 向右平移4个单位车道,再向下平移6个单位车道得到点
向右平移4个单位车道,再向下平移6个单位车道得到点![]() ,
,
∴![]() ,
,![]() ,
,
解得:![]() ,
,![]() .
.
故答案为:3,1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1∥l2∥l3 , 一等腰直角三角形ABC的三个顶点A,B,C分别在l1 , l2 , l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则
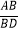 的值为( )
的值为( )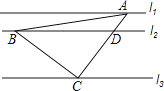
A.
B.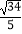
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
 (a>0,a为常数)和y=
(a>0,a为常数)和y=  在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=  的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=  的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y=  的图象于点B,当点M在y=
的图象于点B,当点M在y=  的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积不变;
③当点A是MC的中点时,则点B是MD的中点.
其中正确结论的个数是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )

A. △AFD≌△DCE B. AF=
 AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ABE绕点
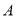 顺时针旋转90
顺时针旋转90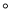 后,得到△ACF,连接DF.下列结论中:①∠DAF=45° ②△
后,得到△ACF,连接DF.下列结论中:①∠DAF=45° ②△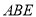 ≌△
≌△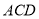 ③AD平分∠EDF ④
③AD平分∠EDF ④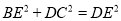 ;正确的有______________(填序号)
;正确的有______________(填序号)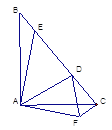
相关试题

