【题目】(10分)将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2![]() ,P是AC上的一个动点.
,P是AC上的一个动点.

(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时□DPBQ的面积.
参考答案:
【答案】(1)DP的长为![]()
(2)∠PDA的度数为75°;
(3)点CP长为![]() 时,此时□DPBQ的面积为
时,此时□DPBQ的面积为![]()
【解析】解:在Rt△ABC中,AB=2![]() ,∠BAC=30°,∴BC=
,∠BAC=30°,∴BC=![]() ,AC=3.
,AC=3.
(1)如图(1),作DF⊥AC,∵Rt△ACD中,AD=CD,∴DF=AF=CF=![]() .
.
∵BP平分∠ABC,∴∠PBC=30°,∴CP=BC·tan30°=1,∴PF=![]() ,∴DP=
,∴DP=![]() =
=![]() .
.
(2)当P点位置如图(2)所示时,根据(1)中结论,DF=![]() ,∠ADF=45°,又PD=BC=
,∠ADF=45°,又PD=BC=![]() ,∴cos∠PDF=
,∴cos∠PDF=![]() =
=![]() ,∴∠PDF=30°.
,∴∠PDF=30°.
∴∠PDA=∠ADF-∠PDF=15°.
当P点位置如图(3)所示时,同(2)可得∠PDF=30°.
∴∠PDA=∠ADF+∠PDF=75°.
(3)CP=![]() .
.
在□DPBQ中,BC∥DP,∵∠ACB=90°,∴DP⊥AC.根据(1)中结论可知,DP=CP=![]() ,∴S□DPBQ=
,∴S□DPBQ=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在正方形ABCD中,对角线AC、BD交于点O,动点P在线段BC上(不含点B),∠BPE=
 ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)如图②,当点P与点C重合时,求证:△BOG≌△POE;
(2)通过观察、测量、猜想: = , 并结合图①证明你的猜想;
= , 并结合图①证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图②),若∠ACB=a,直接写出 的值,为 . (用含a的式子表示)
的值,为 . (用含a的式子表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
(1)请你根据左图填写右表:
销售公司
平均数
方差
中位数
众数
甲
9
乙
9
17.0
8
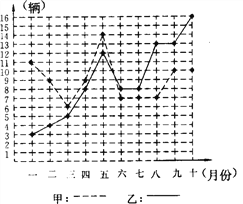
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势
看(分析哪个汽车销售公司较有潜力).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别延长□ABCD的边CD,AB到E,F,使DE=BF,连接EF,分别交AD,BC于G,H,连结CG,AH.
求证:CG∥AH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类
A
B
C
D
E
出行方式
共享单车
步行
公交车
的士
私家车

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4cm,AD=12cm,P点在AD边上以每秒1cm的速度从A向D运动,点Q在BC边上,以每秒4cm的速度从C点出发,在CB间往返运动,二点同时出发,待P点到达D点为止,在这段时间内,线段PQ有( )次平行于AB.

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD面积为( )
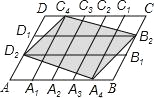
A. 2 B.
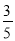 C.
C.  D. 15
D. 15
相关试题

