搜索
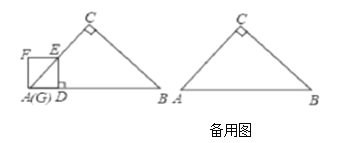
【题目】如图，在
中，
，
，
，线段
上一动点
，以
的速度从点
出发向终点
运动．过点作
，交折线
于点
，以
为一边，在左侧作正方形
．设运动时间为
，正方形与
重叠部分面积为
．
（1）
________
；
（2）当
为何值时，点
在
上；
（3）求
与之间的函数关系式，并写出自变量的取值范围；
（4）直线
将面积分成
两部分时，直接写出的取值范围．
【答案】（1）
；（2）
；（3）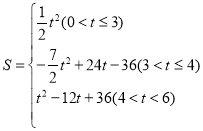
；（4）当点E在AC上时，
；当点E在BC上时，
【解析】
（1）根据题意，设AC长为
，然后利用勾股定理进一步列出方程求解即可；
（2）根据题意，画出当点F在AC上时的图形，然后证明出AG=DG=BD=
AB=2，最后进一步计算即可；
（3）根据题意，分当
时、
时、当
时三种情况，分别得出相应的图形，然后根据图形进一步计算求解即可；
（4）如图所示，①当点E在AC上时，画出此时的正方形DEFG，连接BF交AC于点M，
根据题意首先求出
，然后进一步证明△FEM~△BAM，接着利用相似三角形性质进一步求解即可；②当点E在BC上时，，画出此时的正方形DEFG，延长BF交AC于点M，过点F作FN⊥BC交BC于N，首先根据等腰直角三角形性质得出BD=DE=EF=
，NE=FN=
，然后进一步证明△BFN~△BMC，从而得出
，由此进一步分析即可得知当直线
将
面积分成
两部分时的
的取值范围.
（1）设AC长为，则BC=，
则在Rt△ABC中，
，
即：
，
解得：
，
∵
是正数，
∴
，
∴AC=
，
故答案为：；
（2）当点F在AB上时，可得下图：
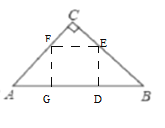
∵四边形DEFG是正方形，
∴EF∥AB，EF=FG=GD=ED，∠FGA=∠EDB=90°，
∵在Rt△ABC中，AC=BC，∠C=90°，
∴∠B=∠A=45°，
∴△AGF与△BDE是等腰直角三角形，
∴AG=GF，DE=BD，
∴AG=DG=BD=AB=2，
∴AD=4，
∴此时
；
（3）如图，当时，重叠部分为△ADE，
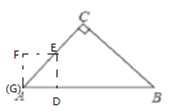
∵∠C=90°，AC=BC，
∴∠CAB=∠B=45°，
∵DE⊥AB，
∴∠AED=45°，
∴AD=DE=，
∴
；
如图，当时，重叠部分是五边形MNEDG，
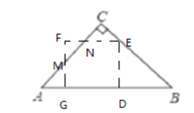
∵四边形DEFG是正方形，
∴FG=GD=DE，∠AGM=∠EDB=∠F=90°，
∵∠B=∠A=45°，
∴∠AMG=∠DEB=45°，
∴AG=GM，BD=DE，
∴FG=DG=DE=DB=，
∴MG=AG=ADDG=
，
∴FM=FGMG=
，
∵∠AMG=45°，∠F=90°，
∴∠FNM=45°，
∴FN=FM=，
∴
如图，当时，重叠部分为正方形DEFG，
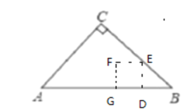
∵四边形DEFG是正方形，
∴GD=DE，∠EDB=90°，
∵∠B=45°，
∴∠DEB=45°，
∴DE=DB=，
∴
，
综上所述，；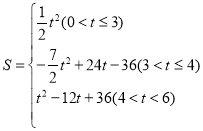
（4）
①如上图所示，当点E在AC上时，画出此时的正方形DEFG，连接BF交AC于点M，
∵要使直线将面积分成两部分，
∴此时
，
∴
，
∴，
∵EF∥AB，
∴∠FEM=∠BAM，
∴△FEM~△BAM，
∴
，
又∵在等腰Rt△ADE中，AE=
，
∴
，
∴；
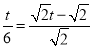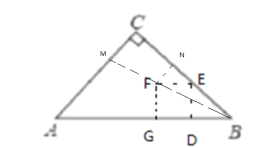
②如上图所示，当点E在BC上时，，画出此时的正方形DEFG，延长BF交AC于点M，过点F作FN⊥BC交BC于N，
则BD=DE=EF=，
在Rt△BDE中，∠ABC=45°，
∴BE=
BD=
，
∵EF∥AB，
∴∠NEF=∠CBA=45°，
∵FN⊥BC，
∴△FNE为等腰直角三角形，
∴NE=FN=，
∵∠C=∠FNB，∠CBM=∠NBF，
∴△BFN~△BMC，
∴
，
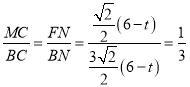∵AC=BC，
∴，
∴
，
∴
，
∴当直线将面积分成两部分时，，
综上所述，当点E在AC上时，；当点E在BC上时，.
