【题目】已知如图,抛物线与轴交于点A和点C（2,0），与 轴交于点D，将△DOC绕点O逆时针旋转90°后，点D恰好与点A重合，点C与点B重合.

（1）直接写出点A和点B的坐标；

（2）求和的值；

（3）已知点E是该抛物线的顶点，求证：AB⊥EB.

【答案】（1）A（-6,0）、B（0,2）；（2）,；（3）E(-2，8) .

【解析】

试题

（1）由题意易得点D的坐标为（0，6），结合AOB是由△DOC绕点O逆时针旋转90°得到的，即可得到OA=6，OB=OC=2，由此即可得到点A和点B的坐标；

（2）将点A和点C的坐标代入列出关于的二元一次方程组，解方程组即可求得的值；

（3）由（2）中所得的值可得二次函数的解析式，把解析式配方即可求得点E的坐标，结合点A和点B的坐标即可求得AE2、AB2、BE2的值，这样由勾股定理的逆定理即可得到∠ABE=90°，从而可得AB⊥BE.

试题解析：

（1）∵在中，当时，，

∴点D的坐标为（0，6），

∵△AOB是由△DOC绕点O逆时针旋转90°得到的，

∴OA=OD=6，OB=OC=2，

∴点A的坐标为（-6，0），点B的坐标为（0，2）；

（2）∵点A（-6，0）和点C（2，0）在的图象上，

∴ ，解得： ；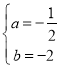

（3）如图，连接AE，

由（2）可知，

∴，

∴点E的坐标为（-2，8），

∵点A（-6，0），点B（0，2），

∴AE2=，AB2=，BE2=，

∴AE2=AB2+BE2，

∴∠ABE=90°，

∴AB⊥EB.

关闭