【题目】已知∠MAN=90°,在射线AM上取一点B,在射线AN上取一点C,连接BC,再作点A关于直线BC的对称点D,连接AD、BD,移动点C,当2AD=BC时,∠ABD的度数是_____.

参考答案:
【答案】30 或150
【解析】
分两种情况,取BC的中点E,连接AE,DE,依据直角三角形斜边上中线的性质,即可得到△ADE是等边三角形,进而依据轴对称的性质得出∠ABD的度数.
解:分两种情况:
如图,当AB>AC时,取BC的中点E,连接AE,DE,
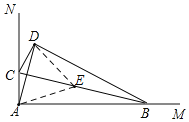
则AE=DE=![]() BC,
BC,
即BC=2AE=2DE,
又∵BC=2AD,
∴AD=AE=DE,
∴△ADE是等边三角形,
∴∠AED=60°,
又∵BC垂直平分AD,
∴∠AEC=30°,
又∵BE=AE,
∴∠ABC=![]() ∠AEC=15°,
∠AEC=15°,
∴∠ABD=2∠ABC=30°;
如图,当AB<AC时,同理可得∠ACD=30°,
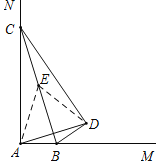
又∵∠BAC=∠BDC=90°,
∴∠ABD=150°,
故答案为:30°或150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
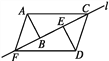
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:
小青:OE=OF;小何:四边形DFBE是正方形;
小夏:S四边形AFED=S四边形FBCE;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是( )

A. 小青 B. 小何 C. 小夏 D. 小雨
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2
 ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图:
(1)如图1,△ABC在边长为1的正方形网格中:
①画出△ABC关于直线l轴对称的△DEF(其中D、E、F分别是A、B、C的对应点);
②直接写出△ABC中AB边上的高= .
(2)如图2,在四边形ABCD内找一点P,使得点P到AB、AD的距离相等,并且点P到点B、C的距离也相等.(用直尺与圆规作图,不写作法,保留作图痕迹).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD平分∠ACB交AB于点D,E为AC上一点,且DE∥BC

(1)求证:DE=CE;
(2)若∠A=90°,S△BCD=26,BC=13,求AD.
相关试题

