【题目】如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是 . 
参考答案:
【答案】![]()
【解析】解:如图1,过E作PQ⊥DC,交DC于P,交AB于Q,连接BE, 
∵DC∥AB,
∴PQ⊥AB,
∵四边形ABCD是正方形,
∴∠ACD=45°,
∴△PEC是等腰直角三角形,
∴PE=PC,
设PC=x,则PE=x,PD=4﹣x,EQ=4﹣x,
∴PD=EQ,
∵∠DPE=∠EQF=90°,∠PED=∠EFQ,
∴△DPE≌△EQF,
∴DE=EF,
易证明△DEC≌△BEC,
∴DE=BE,
∴EF=BE,
∵EQ⊥FB,
∴FQ=BQ= ![]() BF,
BF,
∵AB=4,F是AB的中点,
∴BF=2,
∴FQ=BQ=PE=1,
∴CE= ![]() ,
,
Rt△DAF中,DF= ![]() =2
=2 ![]() ,
,
∵DE=EF,DE⊥EF,
∴△DEF是等腰直角三角形,
∴DE=EF= ![]() =
= ![]() ,
,
∴PD= ![]() =3,
=3,
如图2,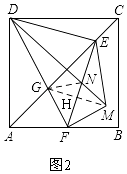
∵DC∥AB,
∴△DGC∽△FGA,
∴ ![]() =
= ![]() =2,
=2,
∴CG=2AG,DG=2FG,
∴FG= ![]() ×
× ![]() =
= ![]() ,
,
∵AC= ![]() =4
=4 ![]() ,
,
∴CG= ![]() ×
× ![]() =
= ![]() ,
,
∴EG= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
连接GM、GN,交EF于H,
∵∠GFE=45°,
∴△GHF是等腰直角三角形,
∴GH=FH= ![]() =
= ![]() ,
,
∴EH=EF﹣FH= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴∠NDE=∠AEF,
∴tan∠NDE=tan∠AEF= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴EN= ![]() ,
,
∴NH=EH﹣EN= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
Rt△GNH中,GN= ![]() =
= ![]() =
= ![]() ,
,
由折叠得:MN=GN,EM=EG,
∴△EMN的周长=EN+MN+EM= ![]() +
+ ![]() +
+ ![]() =
= ![]() ;
;
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
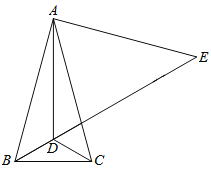
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=30°,点D是△ABC内一点,DB=DC,∠DCB=30°,点E是BD延长线上一点,AE=AB.
(1)求∠ADE的度数;
(2)求证:DE=AD+DC;
-
科目: 来源: 题型:
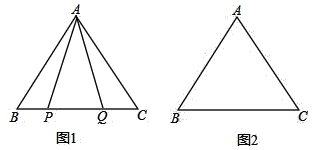
查看答案和解析>>【题目】在等边△ABC中,
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;②小明通过观察、实验,提出猜想:在点P,Q运动的过程中,始终有PA=PM,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证PA=PM,只需证△APM是等边三角形.
想法2:在BA上取一点N,使得BN=BP,要证PA=PM,只需证△ANP≌△PCM.……
请你参考上面的想法,帮助小明证明PA=PM(一种方法即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
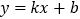 的图象如图,则下列说法:①
的图象如图,则下列说法:①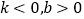 ;②
;② 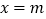 是方程
是方程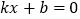 的解;③若点
的解;③若点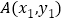 ,
,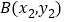 是这个函数的图象上的两点,且
是这个函数的图象上的两点,且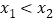 ,则
,则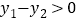 ;④当
;④当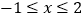 ,函数的值
,函数的值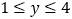 ,则
,则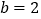 .其中正确的个数为( )
.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索与发现:
(1)若直线a1⊥a2,a2∥a3,则直线a1与a3的位置关系是__________,请说明理由.
(2)若直线a1⊥a2,a2∥a3,a3⊥a4,则直线a1与a4的位置关系是________.(直接填结论,不需要证明)
(3)现在有2 011条直线a1,a2,a3,…,a2 011,且有a1⊥a2,a2∥a3,a3⊥a4,a4∥a5…,请你探索直线a1与a2 011的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图象(折线OEFPMN)描述了某汽车在高速公路上行驶过程中速度与时间的函数关系,下列说法中,错误的是( )

A. 第5 min时汽车的速度是80 km/h
B. 从第3 min到第6 min,汽车行驶了4 km
C. 第 6 min到9 min,汽车行驶了6 km
D. 从第9 min到第12 min,汽车一直在减速直到速度减为0 km/h
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完;销售金额与卖西瓜千克数之间的关系如图所示,那么小李赚了_________.元.

相关试题

