【题目】如图,直线y= ![]() x+2与双曲线相交于点A(m,3),与x轴交于点C.
x+2与双曲线相交于点A(m,3),与x轴交于点C. 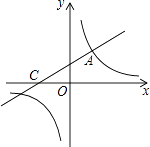
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
参考答案:
【答案】
(1)解:把A(m,3)代入直线解析式得:3= ![]() m+2,即m=2,
m+2,即m=2,
∴A(2,3),
把A坐标代入y= ![]() ,得k=6,
,得k=6,
则双曲线解析式为y= ![]()
(2)解:对于直线y= ![]() x+2,令y=0,得到x=﹣4,即C(﹣4,0),
x+2,令y=0,得到x=﹣4,即C(﹣4,0),
设P(x,0),可得PC=|x+4|,
∵△ACP面积为3,
∴ ![]() |x+4|3=3,即|x+4|=2,
|x+4|3=3,即|x+4|=2,
解得:x=﹣2或x=﹣6,
则P坐标为(﹣2,0)或(﹣6,0)
【解析】(1)把A坐标代入直线解析式求出m的值,确定出A坐标,即可确定出双曲线解析式;(2)设P(x,0),表示出PC的长,高为A纵坐标,根据三角形ACP面积求出x的值,确定出P坐标即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从1名男生和3名女生中随机抽取参加“我爱盐城”演讲比赛的同学.
(1)若抽取1名,恰好是男生的概率为;
(2)若抽取2名,求恰好是2名女生的概率.(用树状图或列表法求解) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A、B两地于上午9点钟同时出发,相向而行,已知甲的速度比乙快2千米/时,到上午11时两车还相距36千米,又过了2小时后,两车又相距36千米.
(1)求甲乙两地间的距离与两车的速度;
(2)若甲乙两车分别从A、B两地同时相向而行,到B、A两地后立即返回,求两车第一次相遇和第二次相遇所走的时间是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
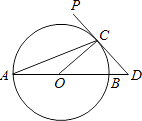
(1)求∠D的度数;
(2)若CD=2,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,以△ABC的边AB、AC为边分别向外作等腰直角△ABD和等腰直角△ACE,连接CD、BE、DE
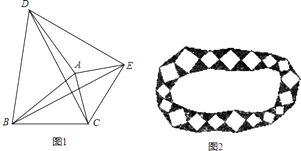
(1)证明:△ADC≌△ABE;
(2)试判断△ABC与△ADE面积之间的关系,并说明理由;
(3)园林小路,曲径通幽,如图2所示,小路由白色的正方形大理石和黑色的三角形大理石铺成,已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地平方米.(不用写过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】今年以来,国务院连续发布了《关于加快构建大众创业万众创新支撑平台的指导意见》等一系列支持性政策,各地政府高度重视、积极响应,中国掀起了大众创业万众创新的新浪潮.某创新公司生产营销A、B两种新产品,根据市场调研,发现如下信息: 信息1:销售A种产品所获利润y(万元)与所售产品x(吨)之间存在二次函数关系y=ax2+bx,当x=1时,y=7;当x=2时,y=12.
信息2:销售B种产品所获利润y(万元)与所售产品x(吨)之间存在正比例函数关系y=2x.
根据以上信息,解答下列问题:
(1)求a,b的值;
(2)该公司准备生产营销A、B两种产品共10吨,请设计一个生产方案,使销售A、B两种产品获得的利润之和最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,∠B=60°,D为AB的中点,∠EDF=90°,DE交AC于点G,DF经过点C.
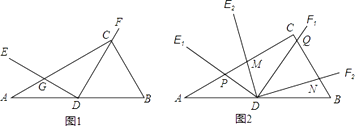
(1)求∠ADE的度数;
(2)如图2,将图1中的∠EDF绕点D顺时针方向旋转角α(0°<α<60°),旋转过程中的任意两个位置分别记为∠E1DF1 , ∠E2DF2 , DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求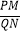 的值;
的值;
(3)若图1中∠B=β(60°<β<90°),(2)中的其余条件不变,判断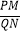 的值是否为定值?如果是,请直接写出这个值(用含β的式子表示);如果不是,请说明理由.
的值是否为定值?如果是,请直接写出这个值(用含β的式子表示);如果不是,请说明理由.
相关试题

