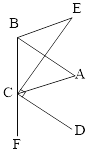
【题目】如图所示,已知BA平分∠EBC, CD平分∠ACF,且![]() ∥CD,
∥CD,
(1)试判断AC与BE的位置关系,并说明理由;
(2)若DC⊥EC于C, 猜想∠E与∠FCD之间的关系,并推理判断你的猜想。
参考答案:
【答案】(1)AC∥BE.理由见解析;(2)∠E与∠FCD互余,理由见解析.
【解析】试题分析:(1)由AB∥CD得到∠ABC=∠DCF,再由BA平分∠EBC, CD平分∠ACF得到∠EBC=2∠ABC,∠ACF=2∠DCF,即可得∠EBC=∠ACF,根据同位角相等得出AC∥BE;
(2)由AC∥BE得到∠E=∠ACE,再由CD平分∠ACF得到∠ACD=∠FCD和DC⊥EC,得到∠ACE+∠ACD=90°,可得出∠E+∠FCD=90°,即∠E与∠FCD互余.
试题解析:
(1)AC∥BE .理由如下:
因为AB∥CD,
所以∠ABC=∠DCF
因为BA平分∠EBC, CD平分∠ACF
所以∠EBC=2∠ABC,∠ACF=2∠DCF
所以∠EBC=∠ACF
所以AC∥BE
(2)∠E与∠FCD互余
因为AC∥BE,所以∠E=∠ACE
因为CD平分∠ACF,所以∠ACD=∠FCD
又因为DC⊥EC,所以∠ACE+∠ACD=90°
所以∠E+∠FCD=90°
即∠E与∠FCD互余
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A 篮球 B 乒乓球C 羽毛球 D 足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
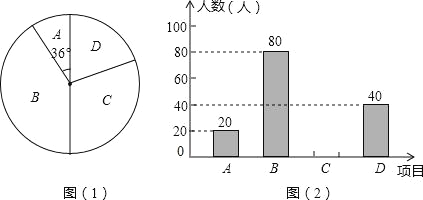
(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
-
科目: 来源: 题型:
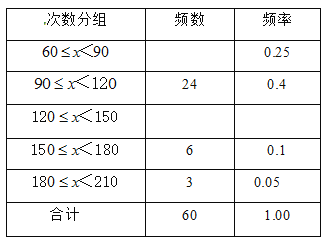
查看答案和解析>>【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面不完全的频数分布表:
(1)补全表中信息
(2)跳绳次数在
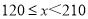 范围的学生占全班学生的百分比是多少?
范围的学生占全班学生的百分比是多少?(3)画出适当的统计图表示上面的信息
-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装参加演出,下面是某服装厂给出的演出服装的价格表:
购买服装的套数
1套至45套
46套至90套
91套及以上
每套服装的价格
60元
50元
40元
如果两校分别单独购买服装,一共应付5000元.
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(2)甲、乙两校各有多少学生准备参加演出?
(3)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出,请为两校设计一种省钱的购买服装方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】到三角形三边距离相等的点是三角形( )的交点。
A. 三边垂直平分线B. 三个内角平分线
C. 三条中线D. 三条高线所在的直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,函数y=﹣x﹣2的图象经过第象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. x3+x3=2x6 B. x6÷x2=x3 C. (﹣3x3)2=2x6 D. x2x﹣3=x﹣1
相关试题

